Editor’s note:
The special column “Statistics in Oncology Clinical Trials” is dedicated to providing state-of-the-art review or perspectives of statistical issues in oncology clinical trials. Our Chairs for the column are Dr. Daniel Sargent and Dr. Qian Shi, Division of Biomedical Statistics and Informatics, Mayo Clinic, Rochester, MN, USA. The column is expected to convey statistical knowledge which is essential to trial design, conduct, and monitoring for a wide range of researchers in the oncology area. Through illustrations of the basic concepts, discussions of current debates and concerns in the literature, and highlights of evolutionary new developments, we are hoping to engage and strengthen the collaboration between statisticians and oncologists for conducting innovative clinical trials. Please follow the column and enjoy.
Phase III design: principles
Introduction
Phase III clinical trials are considered the gold standard to demonstrate the effects of an experimental therapy compared to standard therapy for a disease of interest. For instance, new drugs must typically be shown to have a sufficient level of efficacy and safety in two independent phase III trials before they are approved for marketing by the health authorities. Likewise, new treatments are adopted in clinical practice if they have been tested in at least one well-designed and well-conducted phase III clinical trial. Our purpose in this paper is to discuss the basic considerations to be taken into account when designing a phase III trial. A clinical trial can be defined as a prospective study that uses a specific experimental design (section Experimental design) to investigate the effects of an experimental treatment as compared with a well-known control treatment (section Treatments) in a well-defined population of patients (section Patients) with respect to one or several endpoints of interest (section Endpoints). For lack of space, the present paper can provide only an overview of these issues; the interested reader will find a more comprehensive coverage of these issues, e.g., in the excellent book by Piantadosi (1). Historical trials will be used to illustrate the issues as clearly as possible.
Experimental design
What is the hypothesis of interest?
The purpose of a randomised trial is to test a statistical hypothesis. Most commonly, the hope is to show that the experimental group is better than the control group in terms of a so-called primary endpoint (such as time to disease progression), even though other endpoints may be of major interest as well (such as tolerance to treatment). The statistical approach to showing superiority of the experimental treatment is to test a null hypothesis of no difference, in the hope that the data collected in the trial will convincingly demonstrate this null hypothesis to be incompatible with the data, in which case the null hypothesis can be rejected. For instance, it would be unlikely for time to progression to be much longer in the experimental group than in the control group if there was no real difference between the treatments. The P value of the statistical test carried out at the end of the trial quantifies the probability of a difference as large as that observed if the null hypothesis were true. If the P value is less than some pre-specified probability (referred to as the “significance level”, denoted “α”), then the result is said to be statistically significant. Thus, a P value of less than 5% indicates that it is rather unlikely (less than a chance in 20) that the observed treatment difference is merely due to chance rather than to a true treatment effect, hence such a result is conventionally considered to be statistically significant.
When the control group of a randomised trial is an active therapy considered to be the standard of care, the aim of the trial may be to show that the efficacy of the experimental treatment is at least as good to that of the standard treatment, while being less toxic, better tolerated, more convenient to administer, or less expensive than the standard treatment. In this case, the null hypothesis is that the patients on the experimental treatment do worse than the control group, and again one hopes to be able to reject this null hypothesis. A typical example was the demonstration that the oral fluoropyrimidine capecitabine (Xeloda®) was non-inferior to the standard of care, which consisted of intravenous injections of 5-fluorouracil. The trial showed that the main efficacy endpoints (response rate, time to disease progression and survival) did not differ between the oral and the intravenous drug, but the former had much less toxicity than the latter, making it more clinically attractive (2).
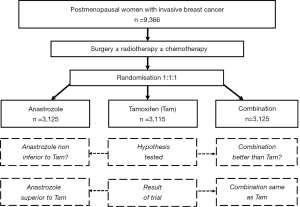
The ATAC trial is an even more interesting example (Figure 1). The trial was designed to show non-inferiority of the aromatase inhibitor anastrozole compared to tamoxifen alone in terms of disease-free survival, and superiority of the combination of anastrozole and tamoxifen over tamoxifen alone. As it turns out, the trial showed that anastrozole was significantly superior to tamoxifen alone, while the combination was no better than tamoxifen alone! These were rather unexpected results compared to the pre-specified hypotheses, but because of the large number of patients included in the trial (over 9,000), these results were established with great statistical confidence (3).
How are patients randomised?
In phase III clinical trials, patients are allocated by a chance mechanism (randomisation) to receive one of the therapies being compared. The fundamental feature of randomisation is to provide comparability of the treatment groups with respect to all known and unknown factors, thus permitting an unbiased comparison between the treatment groups. Many benefits follow directly from randomisation: in a well-conducted trial, any difference observed between the randomised treatment arms is causally due to a treatment effect, or to the play of chance; simple statistical tests provide valid treatment comparisons that are more convincing than adjusted comparisons based on elaborate models; and changes over time in the patient population under study, in diagnostic procedures, or even in evaluation of therapeutic response will affect all randomised groups equally, and will therefore not invalidate the treatment comparisons.
The way in which the various treatments are allocated to the successive patients who enter a phase III trial must be carefully defined. Simple randomisation consists of choosing the treatment at random regardless of patient characteristics. The advantage of simple randomisation, beside simplicity, is that it completely eliminates selection bias since the next treatment assignment is never predictable. The disadvantage of simple randomisation is that it does not protect against an accidental bias that may occur as a result of chance imbalances between the different treatment arms (4).
Stratified randomisation consists of allocating treatments after taking into account important patient characteristics, called stratification factors (e.g., age, sex, disease stage, specific gene mutations, prior therapies, etc.). The purpose of stratified randomisation is to reduce the likelihood of chance imbalances in the treatment assignments among strata. When stratified randomisation is used for prognostic factors (i.e., baseline characteristics that have a major impact on the patient’s prognosis), the potential for accidental bias resulting from imbalances between treatment groups is reduced, the results of the trial may be more convincing because treatment groups look alike in terms of the important prognostic factors, and the precision of the estimates of treatment effect is increased (though the gain is usually quite small). If stratification is adopted, it is advisable to stratify only for factors of known prognostic value. If, for instance, gender were of no prognostic impact on the patient outcome, it would be pointless to stratify for gender. It is also advisable to stratify only for factors that are known with certainty at the time of randomisation. If, for instance, histology were only confirmed several weeks after randomisation, it would be hazardous to stratify for histology. In multicenter trials, center is often treated as a stratification factor, regardless of whether patient prognosis is expected to vary across centers, in order to limit treatment imbalances within each participating center.
Minimization is a dynamic process that takes into account the distribution of prognostic factors of patients already randomized when allocating a treatment to a new patient, in order to minimize the risk of an imbalance between the treatment groups with respect to all these prognostic factors. The major advantage of using minimization is that good treatment balance can be achieved for a large number of stratification factors simultaneously: as an extreme example, in a multicenter trial comparing several anti-emetic therapies, six factors associated with a higher emetic risk, as well as center, were taken into account using minimization, and the distributions of these factors were almost identical among all treatment groups (5).
Treatments
What is the control group?
When designing a randomised phase III clinical trial, it is crucial to identify the appropriate control group to which the experimental treatment group(s) will be compared. An untreated control group is indicated when no standard treatment exists for the disease under consideration, as is sometimes be the case in the adjuvant setting after curative resection of a solid tumor. Many early trials of adjuvant therapy compared an experimental treatment to no further treatment after surgery, but today, the control group typically consists of some standard treatment with established efficacy, called an active control group. Ideally, the control group should receive the standard therapy that would be given outside of a clinical trial setting, but such a standard does not always exist as practices may differ across countries or even across hospitals within the same country. It is sometimes advantageous to let each hospital decide on the control group they feel most comfortable with, because this reflects actual clinical practice, rather than artificial trial conditions. This strategy was chosen (and succeeded) in the EMBRACE trial that compared eribulin monotherapy with currently available treatments in heavily pretreated women with advanced breast cancer (6).
The most reliable form of control treatment consists of a placebo, which is seldom feasible in trials of cytotoxic agents, but should be considered with biological agents such as cytokines, monoclonal antibodies, hormonal agents, etc. that are not expected to induce serious side-effects. In such cases, the treatments may be given in double-blind fashion, whereby neither the physician nor the patient is aware of the treatment (otherwise, the treatment is said to be open-label). The main advantage of double-blind trials is that the assessment of endpoints is completely unbiased by knowledge of the treatment received. The ATAC trial, for instance, was a double-blind trial of tamoxifen alone, anastrozole alone, or the combination of both drugs. Thus, in this trial, every patient was randomised to one of three treatment groups: tamoxifen plus anastrozole placebo, tamoxifen placebo plus anastrozole, or tamoxifen plus anastrozole (3).
What are the experimental groups?
From a statistical standpoint, a simple design comparing two groups (an experimental and a control group) is generally preferable to a design comparing multiple groups because the hypothesis of interest is simple, the interpretation of the trial results is straightforward, and the problem of multiple comparisons is avoided.
A notable exception to the simple design comparing two treatments is the dose-ranging design, in which patients are randomised between several doses of the same drug or combination of drugs. In this case, the aim of the trial is usually to test that the therapeutic response increases with dose. Statistically, this can be done through a test for the slope of the dose-response relationship, a powerful test that does not depend on the number of dose levels tested. When the goal of the trial is to find the most effective dose, each dose is compared to control, and the problem of multiple comparisons must be addressed.
Another case where more than two treatment groups are desirable is factorial designs, in which patients are in fact randomised more than once (although the different randomisations can occur concurrently). Such designs are useful when two or more questions are simultaneously of interest for the same patient population. For instance, a trial in patients with advanced breast cancer simultaneously tested a dose-dense (q 2 weekly) chemotherapy schedule versus a conventional (q 3 weekly) chemotherapy schedule, and sequential versus combination administration of the same agents. Thus each patient in this trial was randomised twice: first, between a dose dense and a conventional schedule, and second, between the sequential or the combination administration (7). The trial showed dose dense chemotherapy schedules to be better than conventional schedules, but the sequential administration did not differ from the combined administration. Under the assumption of no interaction between the two questions, a factorial design allows the investigators to study these two questions with the same number of patients as they would have needed to study either question alone. In other words, studying each question separately would have required twice as many patients as studying them both in a single factorial design. That factorial designs should result in such huge savings in terms of patient numbers is somewhat counter-intuitive, but is merely due to the fact that every patient contributes to both questions independently. Sometimes, however, factorial designs fail because of an interaction between the two questions being investigated. For instance, a trial in patients with resectable colorectal cancer tested simultaneously 5FU + leucovorin vs. 5FU + levamisole, and the duration of either regimen (6 vs. 12 months). Unfortunately, the optimal duration depended strongly on which of the two regimens (5FU + leucovorin or 5FU + levamisole) was administered, so that no general conclusion on the duration of chemotherapy could be drawn from this trial (8).
Yet another case where more than two treatment groups may be desirable is when a new drug is being tested to either replace, or be added to, some existing standard drug. The ATAC trial provides a clear example: factorial design could not be considered for this trial because no patient could be left untreated, hence all patients received either tamoxifen or anastrozole, or both (3).
Patients
What is the target population?
The choice of the appropriate target population is often a matter of heated debate when designing a trial. Indeed, two conflicting arguments come into play: on the one hand, it makes sense to restrict the trial only to patients who may benefit from the intervention, while on the other hand, it seems sensible to open the trial to as many patients as possible, for in the absence of evidence to the contrary, all patients may a priori be assumed to benefit from the experimental treatment, albeit to varying degrees. We examine these two arguments in turn.
A “targeted” approach is warranted if it is known (or thought to be highly likely) that only a subset of patients will benefit. For example, in patients with breast cancer, it is well established that patients benefit from hormonal therapy if and only if their tumors express estrogen receptors (ER+) or progesterone receptors (PR+). It is worth remembering, however, that in early days it was believed that patients not expressing ER nor PR could also benefit from tamoxifen through some cytotoxic (rather than hormonal) effect. The lack of benefit in hormone receptor negative patients has in fact been established reliably through inclusion of such patients in randomised trials.
As tumor biology evolves and drugs are developed for specific molecular targets, there will be more and more situations in which the efficacy (and/or tolerability) of new treatments will be expected to be limited to specific, molecularly defined, patient subsets. Perhaps the most celebrated example of such a situation is that of imatinib (Gleevec®), a selective inhibitor of the Bcr-Abl tyrosine kinase used in chronic-phase myeloid leukaemia patients who are Philadelphia-chromosome positive (9). In these patients, imatinib produced a rate of major cytogenetic response of 87%, versus only 35% in patients treated with a standard regimen of interferon-alpha plus cytarabine. At such outstanding levels of efficacy, large clinical trials are no longer needed to show small, incremental benefits. In the most extreme cases, it has been argued that randomized trials are not needed at all, for instance in situations where no durable response has ever been observed with standard therapy and a new drug produces a number of such responses. Even in these cases, though, the best strategy may be to start a randomized trial, and stop this trial as soon as convincing and statistically reliable evidence has emerged that the new treatment is vastly superior to standard therapy. In reality, there are not many situations in which molecular biology is so clear, and the impact of new drugs on clinically relevant endpoints so pronounced, that no randomized evidence is needed, whether overall or in specific patient subsets. Knowledge about the mechanism of action of new drugs may have been studied in exquisite detail in pre-clinical experiments, and yet remain substantially uncertain in the clinic.
Examples of unexpected findings abound in clinical research. For instance, all the randomized trials of trastuzumab (Herceptin®) as an adjuvant treatment for early breast cancer were restricted to patients with an amplification of the her2-neu gene. A few patients without her2-neu gene amplification were mistakenly included in these trials (these patients were in fact ineligible for the trials). When the effect of trastuzumab was estimated among these ineligible patients, it appeared, contrary to expectation, to be as large as among the patients with gene amplification. The lack of gene amplification in these patients was carefully confirmed independently by a number of central laboratories, so the unexpected result is not due to laboratory errors (10). Whether it is due to tumor heterogeneity or some other biological mechanism is currently uncertain, but this finding prompted a large collaborative group in the US to carry out a confirmation trial to test the hypothesis that trastuzumab may have an effect among patients without her2-neu gene amplification.
In contrast to the targeted approach, a “broad” approach is warranted in the absence of definite knowledge about the factors predicting the therapeutic outcome. For cytotoxic drugs, for example, there is often no reason to believe that the drug will work in some subsets of patients but not in others, and the decision to treat must therefore be based on the benefit/risk ratio for individual patients. In such cases, broad eligibility criteria may be preferred, in order not to exclude patients who might benefit from the experimental treatment. A case in point is the arbitrary age limits that often exclude elderly patients from clinical trials, even if they are otherwise fit to receive either of the treatments under comparison. A better strategy is to let the participating physicians decide on what patients they enter in the trial, based on their clinical judgment. Statistically speaking, when there is doubt about which patients should be included, the choice between restricted vs. broad eligibility criteria can be based on considerations of sample size and trial duration.
Let us take the example of adjuvant therapy for colorectal cancer. Assume a trial is being considered to compare the best available therapy to some experimental therapy. The trial will be open to all patients with stage III disease (tumors with lymph node involvement), but the question is whether it should also be open to patients with stage II tumors (without lymph node involvement), under the assumption that the relative treatment benefit may be the same among patients with stage II and III disease. Patients with stage II disease have a better prognosis, on average, than patients with stage III disease, and therefore the treatment benefit will be smaller in absolute terms among patients with stage II disease. This would argue against their inclusion. However, the trial will obviously take longer to accrue any given sample size if patients with stage II disease are excluded, and therefore there may be situations in which it is preferable to include them anyway. Moreover, it may be of interest to test the benefit of the experimental treatment in both stage II and III disease, even if it takes longer to show the former than the latter. All in all, the only patients who should definitely be excluded from a clinical trial are those who are known not to benefit from therapy. At the present time, knowledge of factors that predict such lack of benefit is still quite limited, but a better identification of molecular heterogeneity will better inform the exclusion of patients in the future, which have a substantial impact on the power of clinical trials to detect real treatment benefits (11).
How many patients are required?
The number of patients included in a comparative trial, called the sample size of the trial, must be sufficient to detect a difference deemed of clinical relevance. The sample size is calculated so as to guarantee that the difference of interest, if real, will be detected with a given probability, called the statistical power of the trial. In order to calculate a sample size, the trialists need to agree on the following design parameters:
- The significance level, also called the “type I error rate”, denoted α: it is the probability that the trial will show an effect of treatment when in reality the treatment does not have any effect (α is usually taken equal to 5% or less);
- The “type II error rate”, denoted β: it is the probability that the trial will fail to show an effect of treatment when in reality the treatment has an effect (β is usually taken equal to 20% or less). The statistical power of the trial is equal to 1-β (usually equal to 80% or more);
- The expected outcome in the control group, which depends on the disease, endpoint, and patient selection;
- The dropout rate, or the proportion of patients who drop out of the trial early;
- The desired outcome in the experimental group, which depends on the disease, endpoint, patient selection, and efficacy of treatment.
Saad has humorously called this the “ABCDE” of calculating a sample size, with A standing for Alpha, B for Beta, C for Control outcome, D for Dropout rate, and E for Experimental outcome (12). Software is available to calculate sample sizes for different types of endpoints, and for different values of the design parameters ABCDE (1).
Many trials in the past have ended up being inconclusive (not showing a statistically significant difference between the treatment groups) because of an insufficient sample size (and ensuing low power). In this case, a meta-analysis of all related trials would be the best way of establishing real, but small, treatment differences (13). The need for large-scale trials has been recognized since; for instance, the ATAC trial randomised over 9,000 patients for the treatment of patients with early breast cancer. Such a large sample size was needed because the goal of the trial was to show that anastrozole was non-inferior to tamoxifen in terms of disease-free survival (i.e., only a small difference between the two regimens would have been accepted if it had been against anastrozole), while being safer than tamoxifen in terms of drug-related endometrial cancer (3).
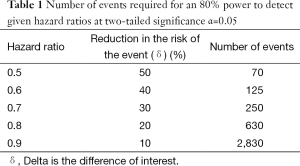
The sample size of a trial depends primarily on the difference of interest, δ, as shown in Table 1. This difference may vary greatly depending on the disease and the treatment considered. For instance, the trial comparing imatinib with interferon-alpha plus cytarabine in myeloid leukaemia was planned to detect an absolute difference of 10% in 5-year progression-free survival rates (assumed to be 50% in the control arm vs. 60% in the experimental arm). In order to detect this difference, a sample size of over 1,000 patients was needed (9). In the actual trial, the benefit observed with imatinib vastly exceeded these expectations, since after only 18 months, the absolute difference in progression-free survival rates was already 18% (74% in the control arm versus 92% in the experimental arm). In retrospect, such a huge treatment benefit could have been seen in far less than 1,000 patients, but the phase III trial had been planned conservatively to detect a smaller difference that would still have been of major clinical importance.
Full table
When the endpoint of interest is a time to event, such as progression-free survival or overall survival, the benefit of an experimental treatment compared to a control treatment is expressed in terms of a hazard ratio, which is equal to the risk of the event in the treatment group divided by the risk of the event in the control group. If the risk is the same in both groups, the hazard ratio is equal to 1. If the treatment reduces the risk of the event, the hazard ratio is less than 1. For instance, a hazard ratio equal to 0.7 corresponds to a 30% =(1–0.7) reduction in the risk of the event. The power of a trial to detect the effect of a treatment on a time to event endpoint depends only on the number of events, and not on the number of patients. Hence for a rare event, many more patients will be needed to achieve the same number of events as for a common event, which is one reason why trials in the adjuvant setting have to be large. Table 1 shows the number of events required to detect given hazard ratios. The number of patients required to observe this number of events depends on the risk of the event, the duration of accrual into the trial, and the duration of follow-up.
Can the trial be stopped early?
The trial of imatinib provides an interesting example of a treatment being far more effective than anticipated. In such situations, there is an ethical imperative to stop the trial as soon as there is enough evidence that the experimental treatment is efficacious and safe. For this reason, most phase III trials now include interim analyses of efficacy. The most common class of designs plans for a sequence of interim analyses to be performed when groups of patients have reached the endpoint of interest—hence these designs are collectively called “group sequential designs” (14). The interim analyses of efficacy are carried out at pre-specified significance levels that are calculated in such a way that the overall significance level for the whole trial remains lower the nominal level desired—say 5%. Typically, the significance levels used for the interim analyses are very small, such that an interim analysis is declared statistically significant only if an extreme treatment effect has already been demonstrated, making the continuation of the trial unnecessary and potentially unethical. It is appropriate to use extreme levels of significance to stop a trial early to safeguard against the play of chance which could cause an apparent but spurious treatment effect at one of the interim analyses.
Sometimes phase III trials must be stopped early for the opposite reason, i.e., when an interim analysis shows that the treatment has a negative effect, or no effect, or much less effect than anticipated, such that continuation of the trial would be very unlikely to result in a proof of efficacy. Here again, interim analyses must be carefully planned, e.g., using group sequential designs, and interpreted with great caution. The interim analyses are usually examined by an Independent Data Monitoring Committee (IDMC), sometimes called Data and Safety Monitoring Board (DSMB) (15). The main advantage of an independent committee is to keep investigators blinded to the interim results of the trial, thereby avoiding any bias that knowledge of interim results could create if the investigators were privy to such results, such as a change in the type of patients entered in the trial. Further information about DSMBs is provided in the paper by Wittes in this special series (16).
Are there subsets of interest?
A prognostic factor is a patient characteristic that modifies his or her prognosis: for instance, patients with a tumor nodal involvement tend to fare less well than those without such involvement. A predictive factor is a patient characteristic that modifies the effect of a treatment: for instance, breast cancer patients without hormone receptors do not benefit from tamoxifen therapy, while patients with hormone receptors do. It is obviously of interest to identify subsets of patients who do not benefit from treatment, or conversely the subset that benefits the most, but the search for subsets is a perilous statistical exercise (17). Indeed, in a clinical trial, the probability of finding a statistically significant result just by chance (if there were no real difference between the treatments being compared) is equal to α, the significance level. This level is set conventionally at 5%, which means that on average one trial in 20 will falsely claim that a difference exists when there is none (a “false positive” claim). This calculation assumes that just one comparison is performed. If multiple comparisons are performed, the probability of false positive claims is increased. Thus, if two subsets are looked at, three treatment comparisons are performed: one overall, plus one in each subset. If each of these comparisons is performed using the conventional 5% significance level, the overall significance level will be increased to more than 14%. If twenty subsets are looked at, the overall significance level will exceed 65%, and thus it will be more likely than not that at least one subset will show a “statistically significant” treatment effect even if there is no true difference in any of the analyses performed. This explains why inappropriate subset claims create enormous confusion in the clinical literature. Simon (18) proposed useful guidelines to assess subset results 25 years ago, but his guidelines remain just as relevant today (Table 2).

Full table
Another important consideration when interpreting subset analyses is to examine the biological plausibility of the findings. The most convincing examples are molecular alterations (such as gene mutations, translocations, amplifications, etc.) that drive the tumor process and may, as such, define subsets that clearly respond or fail to respond to treatment. Even then, however, biology may be incompletely understood and suggest a modulation of the treatment effect that may turn out not to be correct. Here again, confirmation of the hypothesis can be obtained in a randomized trial in which either an interaction test or a prospective subset analysis is planned in addition to the overall analysis.
The latter approach (prospective subset analysis) was used in the SATURN trial for patients with advanced non-small cell lung cancer. After standard treatment with four cycles of platinum-based chemotherapy, patients who had not yet progressed were randomly allocated to receive erlotinib or placebo until progression or unacceptable toxicity (19). Progression-free survival after randomization was tested in all patients at a significance level of 0.03, and in the patients whose tumors had EGFR protein over-expression at a significance level of 0.02. In this trial the overall significance level was clearly maintained at 0.05 (the sum of 0.03 and 0.02), which is in fact conservative because of the correlation between the two tests (overall and in the subset). However the trial showed the same treatment effect overall and in the subset, and it became clear after the trial was completed that while overexpression of EGFR did not increase the efficacy of erlotinib, a specific mutation of the EGFR gene did (20). This example demonstrates that most hypotheses need prospective confirmation, whether suggested by tumor biology or by unexpected statistical evidence from a clinical trial or a patient series. The ideal scenario is one in which several trials show concordant subset results, in which case a combined analysis of all available evidence may be sufficient to establish the validity of a predictive biomarker. This situation led to a change in label by the US Food and Drug Administration (FDA) to restrict usage of the two anti-EGFR monoclonal antibody drugs panitumumab (Vectibix) and cetuximab (Erbitux) to the treatment of patients with K-ras wild type metastatic colorectal cancer (21).
Endpoints
How are the patients followed-up?
All patients who are randomised in a phase III trial should be followed according to the study protocol, even if they are found, after randomisation, to be ineligible or invaluable for any reason. The most reliable analysis of a trial is based on the intent-to-treat principle, which consists of considering all randomised patients, regardless of any protocol violations. In particular, patients who take other treatments or refuse any treatment have to be kept in the treatment group they were randomized to. All other forms of analysis may be biased and, as such, are less desirable from a statistical viewpoint. In an intent-to-treat analysis, the number of patients who drop out of the trial prior to reaching the endpoint of primary interest should be kept to an absolute minimum.
A phase III trial protocol should be precise and detailed, but it should not attempt to provide exhaustive guidelines for all aspects of patient management, since many of the routine examinations and procedures that would be performed outside of the clinical trial contribute no useful information to the endpoints of the trial. Likewise, in a phase III trial, it is generally undesirable to submit the patients to a more thorough or precise follow-up than what they would receive in routine clinical practice, so long as the endpoints of interest are assessed reliably.
Follow-up should be identical in thoroughness and frequency in the various treatment groups. For instance, seeing experimental arm patients more frequently than control arm patients could bias the assessment of disease-free interval, because recurrences would be detected earlier in the experimental group. Softer endpoints, such as disease recurrence, are more subject to bias than harder endpoints, such as death. For instance, if an untreated control group is compared to a treatment group, there may be pressure to scrutinize the untreated patients much more thoroughly than the treated ones in order to identify and treat disease recurrences as early as possible. When end-points are subjective, they should ideally be assessed blindly, i.e., by investigators not aware of the treatment actually received, but this practice has limited applicability in clinical trials of treatments with noticeable side-effects and toxicities.
What are the endpoints of interest?
The ideal endpoint for a phase III trial is one that is important to the patient, observed soon after treatment inception, clinically meaningful, statistically sensitive to treatment effects, and measured objectively and without bias. If such an endpoint existed, it could always serve as the primary endpoint of randomised trials (the primary endpoint is that used to calculate the sample size, and to determine whether the trial shows a significant effect of treatment or not). Unfortunately, in general, no single endpoint fulfils all these desirable conditions. This is illustrated by the endpoints commonly used in advanced cancer: response to treatment (tumor shrinkage), time to disease progression, and overall survival (Table 3). Endpoints based on tumor measurements are usually defined using a set of standardized criteria known as Response Evaluation Criteria in Solid Tumours (RECIST) (22).

Full table
In general, response to treatment (tumor shrinkage) is insufficient per se to establish patient benefit, time to disease progression is hard to measure objectively, and survival is insensitive to true treatment differences (23). Usually, therefore, all of these endpoints are generally analysed and the totality of the evidence is taken into account to support claims of treatment benefit. Whenever possible, attempts are also made to measure the patient’s quality of life, or at least some aspects of symptom-related quality of life. In some advanced forms of cancer (e.g., pancreas), “clinical benefit” has been quantified using scales that combine performance status, weight loss and use of analgesics. Changes on such clinical benefit scales constitute meaningful outcomes to the patients and may be quite sensitive to real treatment effects. As such, they seem useful and often more relevant than general-purpose quality of life questionnaires that do not specifically reflect the effects of treatment.
In some situations, biomarkers are also available to follow the disease status, such as prostate-specific antigen (PSA) and circulating tumor cells (CTC) in patients with prostatic cancer. An issue of major interest is the identification of surrogate endpoints based on these tumor-related markers, which, if valid, would allow trialists to replace a distant endpoint (such as the patient’s death) by endpoints or markers that are observed earlier in the course of the disease (such as sustained changes in a set of markers). For a surrogate endpoint to be valid, two conditions should be fulfilled: first, the surrogate endpoint must be predictive of the true endpoint for individual patients, and second, the treatment effect on the surrogate endpoint must be predictive of the treatment effect on the true endpoint for groups of patients (24). Unfortunately, few endpoints or markers qualify as valid surrogates for the clinical endpoints of interest in advanced disease (25). For instance, in advanced colorectal cancer, tumor response is highly predictive of longer survival in individual patients, but the effects of treatment on tumor response do not reliably predict the effects of treatment on survival (26). Hence, even if an experimental treatment induced higher response rates in advanced colorectal cancer, its effect on survival would remain elusive. Likewise, in prostate cancer, changes in PSA predict the course of the disease and eventually the patient survival, but the effects of treatment on PSA changes have not shown to be predictive of the effects of treatment on survival (27). The discovery of markers that reflect relevant biological mechanisms at the tumor level will undoubtedly make the search for surrogate markers more promising in the future. Until such time, some endpoints measured earlier than death (such as disease-free survival in the adjuvant setting) have been shown to be excellent surrogates for survival (28).
How are the endpoints compared?
The choice of an appropriate method of statistical analysis is crucial for any trial, in particular for phase III trials. This choice is fairly standardized, however, depending on the type of endpoint that is used to assess treatment benefit. Table 4 shows commonly used methods of analysis for normal, binary, or time-to-event endpoints. These methods are available in all standard statistical analysis packages.

Full table
How is the treatment effect expressed?
It is also essential, when reporting the results of a phase III clinical trial, to choose a scale on which the treatment effect is expressed. We noted above that when the endpoint of interest is a time to event, the treatment effect is usually expressed as a hazard ratio, but other scales are available to measure the treatment effect, such as the difference between the median time-to-event endpoints between the arms or the difference between the percentage of patients who have had the event at a given time point.
Different scales to measure the treatment effect have their respective pros and cons. Let us illustrate the choice of a scale on a simple example in which the endpoint of interest is an untoward event, and the purpose of a trial is to reduce the incidence of this event from 50% in the control group to some lower percentage in the treated group (Table 5).

Full table
The most commonly used measures of treatment effect are shown in Table 5:
- The absolute risk difference is equal to the difference in the risks of the event in the two treatment groups: in our example, 0.45–0.50=–0.05, i.e., an absolute risk reduction of 5%;
- The relative risk or risk ratio is equal to the ratio of the risks of the event in the two treatment groups: in our example, 0.45/0.50=0.90, i.e., a relative risk reduction of 10% (=1–0.90);
- The odds ratio is equal to the ratio of the odds of the event in the two treatment groups: in our example, (0.45/0.55)/(0.50/0.50)=0.82, i.e., an odds reduction of 18% (=1–0.82);
- The number needed to treat is equal to the inverse of the absolute risk difference: in our example, 1/0.05=20, i.e., on average 20 patients must be treated for one event to be avoided (which should not be taken as meaning that 19 patients out of 20 do not benefit!).
Note from Table 5 that the odds reduction is larger than the risk reduction, which in turn is larger than the absolute risk reduction. This is not a feature of the particular figures chosen in Table 5, it is a general feature that holds true for any treatment effect (other than zero). This fact should be kept in mind when reading a paper, and more importantly when comparing the results of different papers, since these may be expressed on different scales. It has been shown that the same therapeutic benefit may lead to different prescription patterns depending on the scale used to express it, because any benefit seems more impressive when expressed in relative, rather than absolute, terms (29).
Closing thoughts
There is currently far too much emphasis on the administrative tasks required to conduct a trial, and far too little on the trial design itself. Yet a poorly designed trial is likely to fail to answer the question it addresses. The present paper covers basic considerations in trial design; other articles in this volume cover more advanced features such as adaptive and biomarker-based trial designs. While these are increasingly important in personalized medicine, simple randomized trials will continue to serve clinical research well. In addition, each of the statistical principles discussed in this paper may be directly translated without modification to more sophisticated designs.
Acknowledgements
None.
Footnote
Conflicts of Interest: The author has no conflicts of interest to declare.
References
- Piantadosi S. Clinical Trials: A Methodological Perspective, 2nd Edition. New York: Wiley, 2005.
- Van Cutsem E, Twelves C, Cassidy J, et al. Oral capecitabine compared with intravenous fluorouracil plus leucovorin in patients with metastatic colorectal cancer: results of a large phase III study. J Clin Oncol 2001;19:4097-106. [PubMed]
- Baum M, Budzar AU, Cuzick J, et al. Anastrozole alone or in combination with tamoxifen versus tamoxifen alone for adjuvant treatment of postmenopausal women with early breast cancer: first results of the ATAC randomised trial. Lancet 2002;359:2131-9. [PubMed]
- Buyse M. Centralized Treatment Allocation in Comparative Clinical Trials. Applied Clinical Trials 2000;9:32.
- Hulstaert F, Van Belle S, Bleiberg H, et al. Optimal combination therapy with tropisetron in 445 patients with incomplete control of chemotherapy-induced nausea and vomiting. J Clin Oncol 1994;12:2439-46. [PubMed]
- Cortes J, O’Shaughnessy J, Loesch D, et al. Eribulin monotherapy versus treatment of physician’s choice in patients with metastatic breast cancer (EMBRACE): a phase 3 open-label randomised study. Lancet 2011;377:914-23. [PubMed]
- Citron ML, Berry DA, Cirrincione C, et al. Randomized trial of dose-dense versus conventionally scheduled and sequential versus concurrent combination chemotherapy as postoperative adjuvant treatment of node-positive primary breast cancer: first report of Intergroup Trial C9741/Cancer and Leukemia Group B Trial 9741. J Clin Oncol 2003;21:1431-9. [PubMed]
- O’Connell MJ, Laurie JA, Kahn M, et al. Prospectively randomized trial of postoperative adjuvant chemotherapy in patients with high-risk colon cancer. J Clin Oncol 1998;16:295-300. [PubMed]
- O’Brien SG, Guilhot F, Larson RA, et al. Imatinib compared with interferon and low-dose cytarabine for newly diagnosed chronic-phase chronic myeloid leukemia. N Engl J Med 2003;348:994-1004. [PubMed]
- Perez EA, Press MF, Dueck AC, et al. Immunohistochemistry and fluorescence in situ hybridization assessment of HER2 in clinical trials of adjuvant therapy for breast cancer (NCCTG N9831, BCIRG 006, and BCIRG 005). Breast Cancer Res Treat 2013;138:99-108. [PubMed]
- Betensky RA, Louis DN, Cairncross JG. Influence of unrecognized molecular heterogeneity on randomized clinical trials. J Clin Oncol 2002;20:2495-9. [PubMed]
- Saad ED. The ABCDE of sample size calculation. Personal Communication, 2014.
- Peto R, Collins R, Gray R. Large-scale randomized evidence: large, simple trials and overviews of trials. J Clin Epidemiol 1995;48:23-40. [PubMed]
- Jennison C, Turnbull BW. Group Sequential Methods with Applications to Clinical Trials. Chapman and Hall/CRC, 1999.
- Ellenberg S, Fleming TR, DeMets D. Data Monitoring Committees in Clinical Trials: A Practical Perspective. New York: Wiley, 2002.
- Wittes J, Schactman M. On independent data monitoring committees in oncology clinical trials. Chin Clin Oncol 2014;3:40. [PubMed]
- Rothwell PM. Treating individuals 2. Subgroup analysis in randomised controlled trials: importance, indications, and interpretation. Lancet 2005;365:176-86. [PubMed]
- Simon R. Statistical tools for subset analysis in clinical trials. Recent Results Cancer Res 1988;111:55-66. [PubMed]
- Cappuzzo F, Ciuleanu T, Stelmakh L, et al. Erlotinib as maintenance treatment in advanced non-small-cell lung cancer: a multicentre, randomised, placebo-controlled phase 3 study. Lancet Oncol 2010;11:521-9. [PubMed]
- Pao W, Wang TY, Riely GJ, et al. KRAS mutations and primary resistance of lung adenocarcinomas to gefitinib or erlotinib. PLoS Med 2005;2:e17. [PubMed]
- Bokemeyer C, Van Cutsem E, Rougier P, et al. Addition of cetuximab to chemotherapy as first-line treatment for KRAS wild-type metastatic colorectal cancer: pooled analysis of the CRYSTAL and OPUS randomised clinical trials. Eur J Cancer 2012;48:1466-75. [PubMed]
- Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer 2009;45:228-47. [PubMed]
- Di Leo A, Bleiberg H, Buyse M. Overall survival is not a realistic end point for clinical trials of new drugs in advanced solid tumors: a critical assessment based on recently reported phase III trials in colorectal and breast cancer. J Clin Oncol 2003;21:2045-7. [PubMed]
- Buyse M, Molenberghs G, Burzykowski T, et al. The validation of surrogate endpoints in meta-analyses of randomized experiments. Biostatistics 2000;1:49-67. [PubMed]
- Buyse M, Sargent DJ, Grothey A, et al. Biomarkers and surrogate end points--the challenge of statistical validation. Nat Rev Clin Oncol 2010;7:309-17. [PubMed]
- Buyse M, Thirion P, Carlson RW, et al. Relation between tumour response to first-line chemotherapy and survival in advanced colorectal cancer: a meta-analysis. Meta-Analysis Group in Cancer. Lancet 2000;356:373-8. [PubMed]
- Collette L, Burzykowski T, Carroll KJ, et al. Is prostate-specific antigen a valid surrogate end point for survival in hormonally treated patients with metastatic prostate cancer? Joint research of the European Organisation for Research and Treatment of Cancer, the Limburgs Universitair Centrum, and AstraZeneca Pharmaceuticals. J Clin Oncol 2005;23:6139-48. [PubMed]
- Sargent DJ, Wieand HS, Haller DG, et al. Disease-free survival versus overall survival as a primary end point for adjuvant colon cancer studies: individual patient data from 20,898 patients on 18 randomized trials. J Clin Oncol 2005;23:8664-70. [PubMed]
- Bobbio M, Demichelis B, Giustetto G. Completeness of reporting trial results: effect on physicians’ willingness to prescribe. Lancet 1994;343:1209-11. [PubMed]


