Phase II design: history and evolution
Editor’s note:
The special column “Statistics in Oncology Clinical Trials” is dedicated to providing state-of-the-art review or perspectives of statistical issues in oncology clinical trials. Our Chairs for the column are Dr. Daniel Sargent and Dr. Qian Shi, Division of Biomedical Statistics and Informatics, Mayo Clinic, Rochester, MN, USA. The column is expected to convey statistical knowledge which is essential to trial design, conduct, and monitoring for a wide range of researchers in the oncology area. Through illustrations of the basic concepts, discussions of current debates and concerns in the literature, and highlights of evolutionary new developments, we are hoping to engage and strengthen the collaboration between statisticians and oncologists for conducting innovative clinical trials. Please follow the column and enjoy.
Introduction
Phase II studies follow phase I studies, which determine a safe dose of an agent or regimen (1). The objective of a phase II study is to determine whether the new agent or combination regimen has sufficiently promising biologic activity to warrant further (definitive) testing in a phase III study, which establishes clinical efficacy. Historically, it was believed that biologic activity would vary primarily by tumor type, and, therefore, phase II studies were restricted to a particular histology or closely related set of histologies (the uncommon exception being a study of loosely related rare histologies). This is beginning to change, as molecular characteristics, such as driver mutations and molecular pathway defects become therapeutic targets (2). In addition, to maximize the likelihood of seeing biologic activity in the initial phase II studies of an agent, the patient population should be restricted to those with favorable performance status and minimum prior chemotherapy (2). If there is effective standard therapy available for patients, it is sometimes medically justifiable to postpone it and treat patients first with one or two test courses of the experimental agent, utilizing a so-called “window of opportunity” design. After an agent proves its activity in a population with favorable prognostic characteristics, it may undergo further testing in a less favorable population.
In this paper, we outline the history and development of the phase II trial (as used, in particular, in studies of anti-cancer agents and regimens) over the past half century, attempting to elucidate the primary problems addressed and solutions proposed, so as to provide a primer for young investigators and an overview for the more experienced. Many phase II trial designs have been proposed which have, as yet, failed to achieve common use, and this paper is not meant to be an exhaustive review. For a more comprehensive review of current and prior work relating to phase II trials, please see Green (3), Mariani and Marubini (4) and Thall and Simon (5), and, to further understand the phase II trial within the context of clinical testing in phase I, II and III, please see Simon (2).
Single-armed phase II designs
In the late 1950s, there were few effective agents against most forms of cancer, with most proposed agents proving of no benefit. At that time, therefore, the primary role of the phase II trial was to screen out, as quickly as possible, with the least number of patients exposed, clinically ineffective agents (6). This required a short-term endpoint, indicative of clinical benefit and minimally affected by selection bias (the potential for particularly promising patients to be favored in accrual to the trial). Tumor shrinkage was almost universally chosen as the relevant endpoint in this setting. Such trials also required a statistical design that exposed the minimum number of patients to ineffective agents. It was generally considered that a tumor response rate less than 20% was not clinically promising, and in 1961 Gehan (7) suggested that a run of 14 patients with no response was the minimum number necessary to establish with 95% confidence that the true response rate of the agent did not attain the 20% threshold. (In other words, if the true response rate were at least 20%, there would be at least a 95% likelihood of seeing at least one response among 14 patients.) In this case, the trial would be terminated and declared negative. The standard form of Gehan’s design dictated, further, that if at least one response were observed among the initial 14 patients, then an additional 11-16 patients would be treated, to enable estimation of the response rate with a 95% 2-sided confidence interval spanning approximately the observed response rate plus or minus 0.10 (A 95% 2-sided confidence interval of response rates has the following property. In an ideal situation, if we repeat the same experiment under the exact same conditions, we will observe 95% of the time that the interval contains the true response rate).
As effective anti-cancer agents were identified in the 1960s and 1970s, it became apparent that a more comprehensive phase II statistical approach was required, since the Gehan design gave little guidance concerning how to designate an observed response rate as promising or unpromising, nor did it allow for limiting the probability of making an error in such a designation. In 1982, Fleming (8) proposed a 2-stage design that involved prospectively defining the minimum response rate (called p1) that was sufficiently promising that the investigators would wish to recommend, with high probability, further testing of the agent or combination, and, likewise, the maximum response rate (p0) that was sufficiently discouraging that the investigators would wish to recommend, with high probability, no further testing. Furthermore, the design allowed for limiting both the “type I error”, of calling an agent promising if the true response rate was no more than p0, and the “type II error”, of calling the agent not promising when the true response rate was at least p1. The design required that the total sample size of the two stages (n1 + n2) be sufficiently large so that when the investigators designated the minimum number of responses (r2) necessary for declaring the agent worthy of further testing, the study would have the following property: the probability of a false positive (that the number of responses would be at least r2 when the true response rate was no more than p0) and the probability of a false negative (that the number of responses would be less than r2 when the true response rate was at least p1) satisfied the desired type I and type II error bounds, respectively. Finally, the design provided for early stopping after approximately half the patients (n1) had been accrued, if the results were dramatically positive or negative. This required designating bounds r1 and a1 such that if the number of responses among the initial n1 patients was at least r1 or at most a1, the trial would be terminated early and declared positive or negative, respectively. The positive and negative bounds r1 and a1 were chosen to be sufficiently extreme so that the early stopping option had a minimal effect on the type I and type II error rates, which would be obtained from a one stage trial of n1 + n2 patients.
Table 1 provides an example of a Fleming 2-stage design to distinguish between response rates of p1 =20% and p0 =5%, with type I and type II error rates of 5% and 8%, respectively. The total sample size is n1 + n2 =40, and the final threshold value for declaring the trial positive is r2 =5 responses (12.5%). Interim stopping occurs at n1 =20 patients if the number of responses is a1 =0 or at least r1 =4 (20%). We see that these bounds are sufficiently extreme so that the operating characteristics of the 2-stage trial are essentially identical to what they would be without the possibility of early termination.
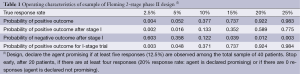
Full table
In 1989, Simon (9) optimized Fleming’s 2-stage design as follows. He suggested that early stopping not be allowed for dramatically positive results, in the interest of achieving more precise estimates of the response rate by accruing to the full sample size in these cases. He also suggested that since most phase II trials were negative, it was appropriate to choose a design that minimized the average sample number (ASN) under the null hypothesis (response rate equal to p0). More precisely, the Simon optimal design is the 2-stage design that minimizes the ASN under the null hypothesis, while maintaining the desired type I and type II error bounds. Such designs are easy to determine, based upon exact binomial calculations, with today’s high-speed computers, and there is a website available to derive them (http://linus.nci.nih.gov/brb/samplesize/otsd.html). Simon optimal designs are to this day considered the standard single-armed phase II design. Table 2 gives designs for four commonly chosen pairs of p0 and p1, with type I and type II error rates set at 0.10 (a standard choice). Based on Table 2, the approximate characteristics shared by the designs are that early termination occurs for response rates less than p0, which occurs with approximately 0.55-0.65 probability under the null hypothesis, and that the trial is declared positive for response rates that are observed at the halfway point between p0 and p1. Simon (9) also gives an alternative 2-stage “minimax design”, which minimizes the total sample size required to achieve the targeted type I and type II error bounds. In general, the total sample size of the 2-stage minimax design will be the same as the required sample size of the corresponding 1-stage design, although there are instances where the 2-stage minimax design actually requires one patient less than the corresponding 1-stage design, due to the discreteness of the binomial distribution and the greater flexibility of the 2-stage design. Simon (9) indicates that there are situations where the minimax design may be preferred over the optimal design, in particular, where the patient population is rare and the anticipated accrual rate is low.

Full table
In choosing an appropriate 2-stage design to use, study investigators have two sets of decisions to make. First, they have to define an appropriate p1 and p0. In cases where there are few, or no effective therapies, p1 is generally chosen to be 20%, the conventional lower bound for a promising response rate. However, where there are a number of effective therapies available, p1 may be set at 30-40%, or higher. In particular, if the phase II trial involves a combination, p1 should be set 10-20% (in absolute terms) higher than what would be attainable with the most active component of the combination. The choice of p0 is dictated by the practical necessity to keep the phase II trial relatively small. This means, in general, setting p0 equal to p1-20% (the exception is setting p0 to 5% when p1 is set to 20%). The second set of decisions involves setting the desired type I (alpha) and type II (beta) error bounds. Common practice is to set both alpha and beta equal to 0.1, since it is generally accepted that in phase II trials, false negative results (which may result in termination of development of a useful agent) are at least as serious as false positive results, which result in wasted time and resources at the phase III level (2). However, in testing agents against solid tumors, where, unfortunately, a large percentage of new agents prove ineffective, many investigators prefer to use an alpha of 0.05, with a beta of either 0.1 or 0.2 (1).
There have been several extensions of the Simon 2-stage design proposed to handle special situations. In 1995, Bryant and Day (10), appreciating the need, in certain cases, for consideration of toxicity issues beyond the phase I trial setting, proposed a design that rejects the new agent if either the response rate is inadequate, or the toxicity is excessive. This design, in particular, allows for limiting accrual to the first stage if the toxicity proves excessive. In 2001, Sargent et al. (11) extended the Simon design to one for which it was possible to formally acknowledge that the response rate fell into an intermediate “borderline” zone for which other considerations were applied to determine whether or not the new agent deserved further testing. A further advantage of this design is that it reduces the required sample size for a given target response difference and given type I and type II error bounds, compared to the Simon design. Also in 2001, Dent et al. (12) proposed a dual-endpoint two-stage design that rejects a new agent if either the response rate is inadequate or the early progression rate is excessive. Analogous to the Bryant and Day design, this design allows for limiting accrual to the first stage if the early progression rate is excessive. Finally, in 2012, appreciating that certain modulating agents were not expected to (necessarily) improve tumor response rate when combined with standard therapy, but were expected to improve progression free survival, Sill et al. (13) proposed a dual-endpoint two-stage design that, in a sense, complemented that of Dent et al. This design allowed for recommending further investigation of an agent that either increased response rate or increased progression-free survival, while allowing for terminating accrual at the first stage if it was already clear that neither improvement was achieved; a characteristic of this design is that it required only modestly greater sample size than a single endpoint design with comparable statistical operating characteristics.
Use of historical controls
The recent rapid evolution in oncology drug development has challenged the previously accepted practice of relying on single-arm phase II trials with a tumor response rate endpoint. Many phase II trials are now designed to assess the promise of a molecularly targeted agent, given either alone or in combination with another regimen. In particular, it is not always anticipated that such agents will produce or improve tumor response rates, rather it may be expected that such agents will improve PFS or OS through means other than direct cell killing as evidenced by tumor shrinkage. In addition, for many diseases, such as lung, colon, breast, and renal cancers (14-16), tumor response has failed to predict for a survival benefit, and for other diseases, such as glioblastoma and prostate cancer, tumor response has proven difficult to measure. Finally, recent papers have demonstrated that even with the use of standard cytotoxic therapy, patients without a tumor response benefit from superior therapy (17).
Based on these considerations, in general, PFS has become in many cases the preferred endpoint for such phase II trials, since it is more statistically efficient than OS (because it is significantly shorter and the treatment effect is not diluted by salvage treatment). For diseases with very short median OS and lack of effective salvage treatment, or where PFS cannot be reliably measured, OS may be a preferred endpoint, even in the phase II setting (18). Such trials can potentially be single-arm studies, with an endpoint of median PFS or OS, or PFS or OS may be measured at a particular time point, and then compared to that of historical controls. There are some strong reasons why statisticians and clinicians historically have favored comparisons with historical controls (over concurrent randomized controls) in phase II trials. Perhaps the strongest reason is statistical efficiency. If there is high confidence that the historical data concerning PFS or OS accurately represent what would be expected of the experimental group if treated in the standard manner, then evaluating the results with an experimental agent or regimen can be done with half the patients or less, by using historical controls rather than concurrent randomized controls. This is true even if there is not access to individual patient historical data, but only the median survival, or if the number of patients in the historic series is limited. In 1982, Brookmeyer and Crowley (19) gave methodology for comparing against historic data, and calculating the required sample size, when only the median survival is available. In 2006, Korn and Freidlin (20) showed how the approach of Rubinstein et al. (21) (who gave methodology for calculating the required sample size for randomized studies using the logrank statistic) could be extended to single-armed studies compared against historical controls, if the patient data are available.
However, the most significant concern with using historical controls to assess PFS or OS in a single-arm phase II trial of an experimental treatment is that the historical controls may not fairly represent the expected outcome of the experimental patients, if given standard treatment. In other words, the historical control patients may be inherently inferior or superior in terms of expected PFS or OS, due to differences with respect to at least three factors. First, the expected outcomes for standard of care may change over time, due to improvements in supportive care, earlier detection, differences in radiological assessment techniques, greater availability of second line therapy (if the endpoint is OS), or other reasons. Second, the inter-institution variability in outcomes has been shown to be large in many settings, thus if the new trial enrolls patients from different institutions, or in a different ratio from the same institutions, the historical data may be inaccurate. Finally, the patients on the new trial may differ from the patients in the historical studies due to differences in prognostic factors. If the important prognostic factors associated with clinical outcome in the patient population can be identified, this last problem may be partially addressed, as demonstrated by Korn et al. (22) in 2008. Using a large meta-analysis of melanoma patients treated on phase II studies, Korn et al. identified the important prognostic variables and their contributions to one-year OS and six-month PFS rates, as well as to the survival distributions for either time-to-event endpoint. This allowed them to construct tests of the observed one-year OS and 6-month PFS rates, or of the respective observed survival distributions, associated with a single-armed test of an experimental regimen, adjusting for the particular mix of prognostic factors in the experimental population. However, even in a detailed meta-analysis of individual patient data, the proportion of variability in outcomes explained by the observed covariates may be limited, which may limit the applicability of this approach.
Randomized studies
For several decades, there has been increased interest in randomized designs for phase II studies in oncology. An increasing number of new agents are biologic or molecularly targeted, and thus are anticipated to yield increased PFS or OS but not necessarily increased tumor shrinkage, alone or, more likely, in combination with standard regimens. PFS or OS is affected by patient characteristics (not always identifiable) which may vary between a new experimental sample and historical control patients. In addition, there is a strong argument for randomization for studies in which the endpoint has been collected differently or inconsistently in the past or is absent from historical data sets. For instance, this could be an endpoint which includes biochemical measures, such as PSA progression in prostate cancer. On the other hand, for some diseases it may be more difficult to accrue patients to a randomized study compared to a non-randomized study at the phase II stage of drug development. Also, in rare disease settings accrual is a challenge. Randomized designs generally require as much as four times as many patients as single-arm studies with similar theoretical statistical operating characteristics. Therefore, there has been a series of attempts to develop randomized designs that offer some protection against the uncertainties and potential biases of single-armed studies, while retaining some of the statistical efficiency.
In 1986, Herson and Carter (23) proposed randomizing a portion of the patients to a small reference arm. The experimental arm would not be compared to the reference arm; it would be analyzed against historical controls as if it were a single-armed study. The reference arm in this design was intended to only act as a check on the similarity of the current patients to the historical controls with respect to clinical outcome when given the standard treatment. The disadvantages of this approach are that the reference arm is too small for its outcome to truly assure comparability for the experimental group, since there is little power to reliably detect a moderate but clinically meaningful lack of comparability. If, in this design, the reference arm has outcome substantially different from that expected based on historical controls, it is difficult to interpret the outcome of the experimental arm. If the reference arm does very poorly compared to controls, an apparently negative outcome for the experimental arm may be due to inferior prognosis for the patients. Conversely, if the reference arm does very well compared to controls, an apparently positive outcome for the experimental arm may be due to superior prognosis for the patients. This is a generic problem with attempting to incorporate a randomized control arm into a phase II trial that is not large enough to allow for direct comparison, to reduce the associated cost in increased sample size.
In 1985, Ellenberg and Eisenberger (24) proposed incorporating a randomized phase II trial as the initial stage in a phase III protocol. The proposal was to terminate the phase III study only if the experimental arm demonstrated inferior tumor response rate to that of the control arm in the phase II stage. In this design, the phase II sample size was specified to be sufficiently large so that there was only a 5% chance that an inferior response rate would occur if the true experimental response rate was superior by some pre-defined amount (this approach could be generalized to use of a PFS endpoint). The disadvantage of this approach is that if the experimental treatment offers no true increase in tumor response rate, the phase III trial will still proceed beyond the initial phase II stage with 0.50 probability. In other words, the initial phase II stage is operating at the 0.50 significance level. This is a generic problem with randomized phase II/III designs; it is very difficult to operate at an appropriate type I and type II error rate without having a large sample size for the phase II portion. In general, this sort of design is appropriate if the investigators are already reasonably certain that the experimental treatment is sufficiently promising to justify a phase III trial, but wish to build into the trial a check on that assumption. In 2009, Hunsberger et al. (25) proposed a somewhat different sort of phase II/III design, where the phase II portion was a randomized phase II trial, with the usual type I error bound of 0.10 (and the usual relatively large sample size, as compared to a single-arm trial), embedded as the first stage in a phase III study. Thall (26) and Korn et al. (27) provide good reviews of randomized phase II/III designs; see also Goldman, LeBlanc and Crowley (28).
Selection designs
There is one context in which the use of a randomized phase II design can achieve its statistical objectives while maintaining a relatively small sample size; this is the case of directly comparing multiple experimental regimens, primarily for the purpose of prioritizing among them for subsequent phase III testing against a control. In 1982, before randomized phase II designs became popular, Simon et al. (29) formalized such pick-the-winner selection designs, where the regimen with the superior observed response rate (by any amount) was chosen, among the two or more compared, for further testing. The original designs were constructed to yield 90% power to detect the superior regimen if the true difference between the response rates was at least 15% (in absolute terms). The weakness in the original design was that it did not assure that the (sometimes nominally) superior experimental regimen was superior to standard therapy. It was occasionally argued that an ineffective experimental regimen could act as a control arm for the other regimen, but the design was not constructed to be used in this way, since, as designed, one of the two or more experimental regimens would always be chosen to go forward, even if neither was superior to standard treatment. To address this, in 2006, Liu, Moon and LeBlanc (30) proposed that each arm of the selection design be constructed as a single-armed two-stage design, to be compared separately against a historically defined response rate, a practice which is now often followed. However, that approach requires that it be possible to compare the experimental regimens to historical controls; this, as we have argued above, is not always the case.
Where the randomized phase II selection design is appropriate, it can be conducted with modest sample size. For example, Simon et al. (29) demonstrated that only 29-37 patients per arm will yield 90% power to detect a regimen that has response rate superior by 15% in a two armed study (see Table 3 for examples of selection designs). In 1993, Liu, Dahlberg and Crowley (31) demonstrated that this approach can be adapted to randomized phase II trials with time-to-event (PFS or OS) endpoints, where the logrank test is used to choose between the two regimens, yielding comparably small sample size requirements. Rubinstein et al. (21) show that the required sample size for such trials is proportional to (zα + zβ)2 where zα and zβ are the standard normal values associated with the type I and type II error bounds, respectively. This means that if the type I error is set to 0.5 (zα =0), as it is for the selection design, then, compared to a randomized study with zα = zβ =0.1 (which is standard for phase 2 designs) with the same targeted hazard ratio, the sample size is reduced by a factor of 4. This means that selection designs constructed to detect a hazard ratio of 1.5 with 90% power are generally similar in size to the original selection designs constructed to detect a response rate difference of 15% with 90% power.
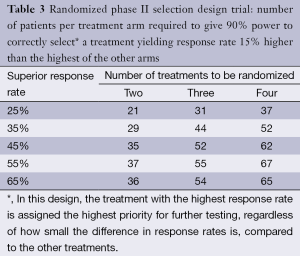
Full table
Randomized phase II screening design
None of the randomized phase II designs described above fully addressed the problem outlined in the beginning of Section “Randomized studies”—the increasing need in oncology to evaluate agents that are anticipated to increase PFS or OS, but not objective tumor response, primarily in combination with standard regimens, where comparison to historical controls may be problematic. The reference arm and phase II/III designs have serious disadvantages, as outlined, and the selection design is meant for the limited situation where experimental regimens are to be compared for prioritization purposes, but, in general, each must also prove itself against historical controls. For this reason, in 2005, Rubinstein et al. (32), building on previous work by Simon et al. (33) and Korn et al. (34), [and similarly to Fleming and Richardson (35)] formalized the randomized phase II screening design. The intention was to define randomized phase II designs that yielded statistical properties and sample sizes appropriate to phase II studies. These designs were meant to enable preliminary comparisons of an experimental treatment regimen, generally composed of a standard regimen with an experimental agent added, to an appropriate control, generally the standard regimen.
Table 4 illustrates the statistical properties of such designs when the endpoint is PFS (or OS), and the logrank test is used. The table provides the required numbers of failures for various type I and type II error rates appropriate to phase II trials, and for various targeted hazard ratios. In general, it is expected that phase II studies will be conducted in patients with advanced disease, where most patients will progress within the trial period, so the required number of failures closely approximates the required number of patients. In the setting of the randomized trial, the usual limits for type I and type II errors may be relaxed; in fact, usage of type I error of 0.20 may be considered in exceptional cases, in particular, in the context of rare disease subgroups. It can also be noted that restricting the trial to a total sample size of no greater than approximately 100 patients restricts the targeted hazard ratio to be at least 1.5.
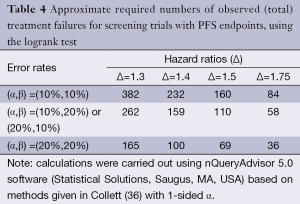
Full table
Table 5 illustrates the statistical properties of such designs when the endpoint is PFS rate, measured at a pre-specified time point, and the binomial proportion test is used. The table provides the required numbers of patients for various type I and type II error rates and for various targeted PFS rate differences (with the equivalent hazard ratios). The table demonstrates that the binomial proportion test, in general, is statistically inefficient compared to the logrank test. In fact, for the same targeted hazard ratio, the comparison of PFS rates at a particular time point requires approximately twice as many patients. Comparing PFS at a particular time point rather than across the entire survival curve means that restricting to a total sample size no greater than approximately 100 patients restricts the targeted hazard ratio to be at least 1.75. Nevertheless, comparing PFS at a pre-specified time is often done since PFS is often considered to be an endpoint that is difficult to measure, potentially subject to investigator bias, or influenced by differential follow-up between the treatment arms.
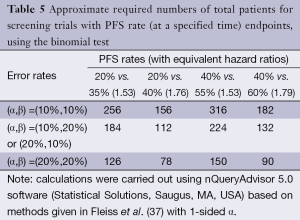
Full table
It must be emphasized that a randomized phase II study should almost never be taken as definitive evidence for the superior efficacy of an experimental agent or regimen. Rubinstein et al. (32) and Fleming and Richardson (35) suggest that the P-value must be less than 0.005 or smaller (a standard cut-off for phase III interim monitoring) for the phase II trial to preclude the necessity for conducting a definitive phase III successor study. Liu et al. (38) demonstrate that small randomized phase II studies can yield substantial false positive rates as well as substantially exaggerated estimated treatment effects. Moreover, as argued by Redman and Crowley (39), in settings where adequate historical controls exist, historically controlled phase II studies are more efficient than randomized studies.
Randomized discontinuation design
An interesting variant of the randomized phase II design, proposed by Rosner et al. (40) in 2006, is the randomized discontinuation design, which initially treats all patients with the study agent for a defined time period, and then randomizes patients with stable disease to continuation or discontinuation for a defined period to assess the effect of the drug in a population of presumably responsive and more homogeneous patients. In 2007, Freidlin and Simon (41) argued that in many settings this design is less efficient than a standard randomized study, due to the large number of patients who must be treated initially, and thus a large number of patients may be unnecessarily exposed to a potentially non-efficacious treatment. On the other hand, they also showed that for the case where a non-identifiable subgroup of patients derives benefit from the treatment, this design may be useful. However, an additional problem with this design is that it may be difficult to define an appropriate population for further study in the event the trial is positive.
PFS vs. OS in randomized phase II studies
An important concern in the design of randomized phase II studies is whether the primary endpoint should be progression-free survival (PFS) or overall survival (OS). There are significant advantages to using PFS, rather than OS, as the primary endpoint in randomized phase II studies. Time-to-progression is shorter than time-to-death, sometimes substantially, so that the PFS endpoint yields more failures and thus greater power for the logrank test. Hazard ratios for PFS are generally greater than for OS, and PFS treatment differences, unlike OS differences, are not diluted by the effects of salvage treatment, both phenomena yielding greater power for the logrank test. Finally, a positive phase II result based on PFS is less likely to complicate randomization to the definitive phase III study than a positive phase II result based on OS. There are, however, also significant disadvantages to using PFS as the primary endpoint. Sometimes PFS is difficult to measure reliably. There may also be concern that evaluation of the endpoint is influenced by investigator treatment bias or differential follow-up by treatment (if the control patients are followed more or less vigilantly, this may bias the observed time of progression). In some cases, the issues of bias can be addressed effectively by blinding the study. If this is not possible, at least the bias associated with differential follow-up can be addressed by using a comparison based on PFS rate at a pre-specified time, rather than using the logrank test. However, as we have demonstrated in Section “Randomized phase II screening design”, this results in substantial loss of statistical efficiency. In 2007, Freidlin et al. (42) addressed this problem by proposing a statistic based on comparing the two treatment arms at two pre-specified time points. They demonstrated that this approach, which also promises to minimize bias due to differential treatment follow-up, recovers most of the efficiency lost in comparison to the logrank test.
Discussion
The increased use of randomized phase II trials has been recommended by European (43,44) and American (32,45) investigators over the past decade, particularly for trials of experimental agents combined with standard regimens, with PFS as the endpoint. An international task force (46) recommended that in “select circumstances”, randomized phase II studies of targeted anticancer therapy are “helpful to define the best dose or schedule, or to test combinations”, but single arm phase II studies continue to be appropriate “when the likely outcomes in the population studied are well described”. In a recent editorial, Ratain et al. (47) took a stronger position, strongly recommending that randomized phase II trials “become a standard approach in oncology, especially for the development of drug combinations.”
The promotion of randomization is already having dramatic effect in the increase in the number of randomized phase II trials. A primary reason for this increase is the appreciation, in the trial design and review process, that even a modest upward drift in the historical control PFS can inflate the type I error rate approximately 3-fold (48). For example, a drift from 50% to 55% in the control 4-month PFS rate, when not accounted for, will increase the type I error of a single-arm Simon optimal (9) trial targeting a 70% 4-month PFS from 0.10 to 0.26. Coupled with this is the realization that such an upward drift over time is relatively likely for PFS as standard of care improves (49).
However, it is also widely accepted that a substantial portion of phase II trials will still be appropriately single-arm (49-52). This includes trials of agents for which tumor regression is anticipated based on mechanism of action, as well as early phase II monotherapy trials to establish a tumor response signal of biological efficacy. Additionally, monotherapy and combination trials with PFS endpoints in diseases with no effective standard therapy and established stable historical controls (e.g., recurrent glioblastoma) can be justified. For OS, an historical database for melanoma has proven useful for designing single arm studies (22). In such situations, adjustment for observed differences in the distribution of known prognostic factors between the historical database and the observed single arm study can reduce potential bias and strengthen inferences.
Importantly, expanding the use of randomization to all phase II situations in which it is appropriate will not by itself maximize the positive predictive value of phase II trials (the probability of a positive phase II trial yielding an agent or combination that is effective by phase III standards). This value is dependent not only on the type I error rates of the phase II trials, but also on the rate of effectiveness (according to the phase II endpoint) of the agents and combinations going into phase II trials for the population of interest, as well as the degree to which the phase II endpoints predict the ultimate phase III endpoints. For example, if the type I and II error bounds are both 0.10, then the positive predictive value of a phase II trial will vary between 32% and 61% in the setting in which (I) the collection of agents and combinations tested is effective, with probability varying between 5% and 15%; and (II) the phase II endpoint is a perfect surrogate for the phase III endpoint. Since stipulation (II) is never the case, the positive predictive value may be substantially less.
We therefore propose four potential approaches to maximizing the effectiveness of phase II trials as predictors for phase III success:
- The pool of agents and combinations going into phase II testing can be enriched for truly active agents. Enrichment may be possible through the increased use of pharmacodynamic assays in phase I and phase 0 testing (53), allowing for go/no-go decisions prior to phase II testing. Additional single arm clinical data (potentially collected at phase I or phase II) may be helpful for screening agents prior to undertaking randomization.
- The subpopulations in which agents and combinations are potentially effective can be better identified so that phase II testing can be limited to such subpopulations. This may be done by increased development and use of pharmacodynamic assays to better characterize the agents (53) and increased development and use of biomarkers to better identify correspondingly sensitive subpopulations of patients (51,52).
- Phase II endpoints that capture and predict a substantial percentage of the treatment effect reflected in the ultimate phase III endpoints can be identified, established, and used (51,54). Such endpoints, including new imaging endpoints, may vary by class of agent and by disease (55,56).
- Even if the approaches listed above are only modestly successful in enriching the pool of phase II agents and combinations so that they are effective, with probability varying between 20% and 40%, the positive predictive value of phase II trials (to reflect true efficacy according to the phase II endpoints) could be increased to between 69% and 86%. How well these phase II trials would then predict phase III efficacy would depend upon the proportion of the phase III treatment effect captured by the phase II endpoint. However, in situations in which the above approaches are not so successful in enriching the pool of phase II agents and combinations, conducting phase II trials at the 0.05 (rather than the 0.10) significance level should be considered. In this way, even if the agents and combinations are effective, with probability varying between 10% and 20%, according to the phase II endpoint, the positive predictive value of phase II trials to reflect true efficacy according to the phase II endpoints would vary between 67% and 82%.
In conclusion, phase II trial design is currently a critically important and evolving area of research, due to the central and growing importance of phase II trials, and there are a number of current issues which we mention here, without elaboration, due to constraints of space. (I) For multi-arm, phase II trials, a number of authors have proposed outcome-adaptive randomization (weighting the randomization, as the trial proceeds, in favor of the arms with superior outcomes) and “borrowing information” across arms (altering the measured outcomes of individual arms by incorporating the results of arms with similar outcomes). Korn and Friedlin (57,58) discuss both of these approaches and cast doubt on their utility; (II) As the use of molecularly targeted therapy increases, the appropriate patient subgroups may become small, creating challenging statistical situations. Korn et al. (59) review the associated problems and potential solutions, with particular relevance to phase II trials; (III) The importance of biomarkers, both prognostic and predictive, is increasing, as a result of the increased use of molecularly targeted therapy. McShane et al. (60) review the problems and potential solutions associated with incorporating biomarkers into phase II trials.
Acknowledgements
Disclosure: The author declares no conflict of interest.
References
- Braun TM. The current design of oncology phase I clinical trials: progressing from algorithms to statistical models. Chin Chin Oncol 2014;3:2.
- Simon R. Design and analysis of clinical trials. In: De Vita VT, Hellman S, Rosenberg SA. eds. Cancer: Principles and Practice of Oncology, ed 11. Philadelphia: Lippincott-Rave, 2011:705-22.
- Green S. Overview of phase II clinical trials. In: Crowley J, Hoering A. eds. Handbook of Statistics in Clinical Oncology (Edition 3). Boca Raton: CRC Press, 2012:109-24.
- Mariani L, Marubini E. Design and analysis of phase II cancer trials (a review of statistical methods and guidelines for medical researchers). Int Stat Rev 1996;64:61-88.
- Thall PF, Simon R. Recent developments in the design of phase II clinical trials. In: Thall PF. eds. Recent Advances in Clinical Trial Design and Analysis. Massachusetts: Kluwer Academic Publishers, 1995;49-71.
- Gehan EA, Schneiderman MA. Historical and methodological developments in clinical trials at the National Cancer Institute. Stat Med 1990;9:871-80; discussion 903-6. [PubMed]
- Gehan EA. The determinatio of the number of patients required in a preliminary and a follow-up trial of a new chemotherapeutic agent. J Chronic Dis 1961;13:346-53. [PubMed]
- Fleming TR. One-sample multiple testing procedure for phase II clinical trials. Biometrics 1982;38:143-51. [PubMed]
- Simon R. Optimal two-stage designs for phase II clinical trials. Control Clin Trials 1989;10:1-10. [PubMed]
- Bryant J, Day R. Incorporating toxicity considerations into the design of two-stage phase II clinical trials. Biometrics 1995;51:1372-83. [PubMed]
- Sargent DJ, Chan V, Goldberg RM. A three-outcome design for phase II clinical trials. Control Clin Trials 2001;22:117-25. [PubMed]
- Dent S, Zee B, Dancey J, et al. Application of a new multinomial phase II stopping rule using response and early progression. J Clin Oncol 2001;19:785-91. [PubMed]
- Sill MW, Rubinstein L, Litwin S, et al. A method for utilizing co-primary efficacy outcome measures to screen regimens for activity in two-stage Phase II clinical trials. Clin Trials 2012;9:385-95. [PubMed]
- Burzykowski T, Buyse M, Piccart-Gebhart MJ, et al. Evaluation of tumor response, disease control, progression-free survival, and time to progression as potential surrogate end points in metastatic breast cancer. J Clin Oncol 2008;26:1987-92. [PubMed]
- Buyse M, Thirion P, Carlson RW, et al. Relation between tumour response to first-line chemotherapy and survival in advanced colorectal cancer: a meta-analysis. Meta-Analysis Group in Cancer. Lancet 2000;356:373-8. [PubMed]
- Goffin J, Baral S, Tu D, et al. Objective responses in patients with malignant melanoma or renal cell cancer in early clinical studies do not predict regulatory approval. Clin Cancer Res 2005;11:5928-34. [PubMed]
- Grothey A, Hedrick EE, Mass RD, et al. Response-independent survival benefit in metastatic colorectal cancer: a comparative analysis of N9741 and AVF2107. J Clin Oncol 2008;26:183-9. [PubMed]
- Ballman KV, Buckner JC, Brown PD, et al. The relationship between six-month progression-free survival and 12-month overall survival end points for phase II trials in patients with glioblastoma multiforme. Neuro Oncol 2007;9:29-38. [PubMed]
- Brookmeyer R, Crowley JJ. A confidence interval for the median survival time. Biometrics 1982;38:29-41.
- Korn EL, Freidlin B. Conditional power calculations for clinical trials with historical controls. Stat Med 2006;25:2922-31. [PubMed]
- Rubinstein LV, Gail MH, Santner TJ. Planning the duration of a comparative clinical trial with loss to follow-up and a period of continued observation. J Chronic Dis 1981;34:469-79. [PubMed]
- Korn EL, Liu PY, Lee SJ, et al. Meta-analysis of phase II cooperative group trials in metastatic stage IV melanoma to determine progression-free and overall survival benchmarks for future phase II trials. J Clin Oncol 2008;26:527-34. [PubMed]
- Herson J, Carter SK. Calibrated phase II clinical trials in oncology. Stat Med 1986;5:441-7. [PubMed]
- Ellenberg SS, Eisenberger MA. An efficient design for phase III studies of combination chemotherapies. Cancer Treat Rep 1985;69:1147-54. [PubMed]
- Hunsberger S, Zhao Y, Simon R. A comparison of phase II study strategies. Clin Cancer Res 2009;15:5950-5. [PubMed]
- Thall PF. A review of phase 2-3 clinical trial designs. Lifetime Data Anal 2008;14:37-53. [PubMed]
- Korn EL, Freidlin B, Abrams JS, et al. Design issues in randomized phase II/III trials. J Clin Oncol 2012;30:667-71. [PubMed]
- Goldman B, LeBlanc M, Crowley J. Interim futility analysis with intermediate endpoints. Clin Trials 2008;5:14-22. [PubMed]
- Simon R, Wittes RE, Ellenberg SS. Randomized phase II clinical trials. Cancer Treat Rep 1985;69:1375-81. [PubMed]
- Liu PY, Moon J, LeBlanc M. Phase II selection designs. In: Crowley J, Ankerst DP. eds. Handbook of Statistics in Clinical Oncology, second edition. Chapman and Hall/CRC, 2006:155-64.
- Liu PY, Dahlberg S, Crowley J. Selection designs for pilot studies based on survival. Biometrics 1993;49:391-8. [PubMed]
- Rubinstein LV, Korn EL, Freidlin B, et al. Design issues of randomized phase II trials and a proposal for phase II screening trials. J Clin Oncol 2005;23:7199-206. [PubMed]
- Simon RM, Steinberg SM, Hamilton M, et al. Clinical trial designs for the early clinical development of therapeutic cancer vaccines. J Clin Oncol 2001;19:1848-54. [PubMed]
- Korn EL, Arbuck SG, Pluda JM, et al. Clinical trial designs for cytostatic agents: are new approaches needed? J Clin Oncol 2001;19:265-72. [PubMed]
- Fleming TR, Richardson BA. Some design issues in trials of microbicides for the prevention of HIV infection. J Infect Dis 2004;190:666-74. [PubMed]
- Collett D. Modeling Survival Data in Medical Research. Chapman & Hall, 1994; Formula 9.2.
- Fleiss JL, Tytun A, Ury HK. A simple approximation for calculating sample sizes for comparing independent proportions. Biometrics 1980;36:343-6.
- Liu PY, LeBlanc M, Desai M. False positive rates of randomized phase II designs. Control Clin Trials 1999;20:343-52. [PubMed]
- Redman M, Crowley J. Small randomized trials. J Thorac Oncol 2007;2:1-2. [PubMed]
- Rosner GL, Stadler W, Ratain MJ. Randomized discontinuation design: application to cytostatic antineoplastic agents. J Clin Oncol 2002;20:4478-84. [PubMed]
- Freidlin B, Simon R. Evaluation of randomized discontinuation design. J Clin Oncol 2005;23:5094-8. [PubMed]
- Freidlin B, Korn EL, Hunsberger S, et al. Proposal for the use of progression-free survival in unblinded randomized trials. J Clin Oncol 2007;25:2122-6. [PubMed]
- Phase II trials in the EORTC. The Protocol Review Committee, the Data Center, the Research and Treatment Division, and the New Drug Development Office. European Organization for Research and Treatment of Cancer. Eur J Cancer 1997;33:1361-3. [PubMed]
- Van Glabbeke M, Steward W, Armand JP. Non-randomised phase II trials of drug combinations: often meaningless, sometimes misleading. Are there alternative strategies? Eur J Cancer 2002;38:635-8. [PubMed]
- Wieand HS. Randomized phase II trials: what does randomization gain? J Clin Oncol 2005;23:1794-5. [PubMed]
- Booth CM, Calvert AH, Giaccone G, et al. Design and conduct of phase II studies of targeted anticancer therapy: recommendations from the task force on methodology for the development of innovative cancer therapies (MDICT). Eur J Cancer 2008;44:25-9. [PubMed]
- Ratain MJ, Humphrey RW, Gordon GB, et al. Recommended changes to oncology clinical trial design: revolution or evolution? Eur J Cancer 2008;44:8-11. [PubMed]
- Tang H, Foster NR, Grothey A, et al. Comparison of error rates in single-arm versus randomized phase II cancer clinical trials. J Clin Oncol 2010;28:1936-41. [PubMed]
- Gan HK, Grothey A, Pond GR, et al. Randomized phase II trials: inevitable or inadvisable? J Clin Oncol 2010;28:2641-7. [PubMed]
- Rubinstein L, Crowley J, Ivy P, et al. Randomized phase II designs. Clin Cancer Res 2009;15:1883-90. [PubMed]
- Stewart DJ. Randomized phase II trials: misleading and unreliable. J Clin Oncol 2010;28:e649-50; author reply e651-3.
- Seymour L, Ivy SP, Sargent D, et al. The design of phase II clinical trials testing cancer therapeutics: consensus recommendations from the clinical trial design task force of the national cancer institute investigational drug steering committee. Clin Cancer Res 2010;16:1764-9. [PubMed]
- Kummar S, Kinders R, Rubinstein L, et al. Compressing drug development timelines in oncology using phase ‘0’ trials. Nat Rev Cancer 2007;7:131-9. [PubMed]
- Sargent DJ, Rubinstein L, Schwartz L, et al. Validation of novel imaging methodologies for use as cancer clinical trial end-points. Eur J Cancer 2009;45:290-9. [PubMed]
- Burzykowski T, Buyse M, Yothers G, et al. Exploring and validating surrogate endpoints in colorectal cancer. Lifetime Data Anal 2008;14:54-64. [PubMed]
- Burzykowski T, Buyse M, Piccart-Gebhart MJ, et al. Evaluation of tumor response, disease control, progression-free survival, and time to progression as potential surrogate end points in metastatic breast cancer. J Clin Oncol 2008;26:1987-92. [PubMed]
- Korn EL, Freidlin B. Outcome--adaptive randomization: is it useful? J Clin Oncol 2011;29:771-6. [PubMed]
- Freidlin B, Korn EL. Borrowing information across subgroups in phase II trials: is it useful? Clin Cancer Res 2013;19:1326-34. [PubMed]
- Korn EL, McShane LM, Freidlin B. Statistical challenges in the evaluation of treatments for small patient populations. Sci Transl Med 2013;5:178sr3.
- McShane LM, Hunsberger S, Adjei AA. Effective incorporation of biomarkers into phase II trials. Clin Cancer Res 2009;15:1898-905. [PubMed]


