Adaptive clinical trial designs in oncology
Editor’s note:
The special column “Statistics in Oncology Clinical Trials” is dedicated to providing state-of-the-art review or perspectives of statistical issues in oncology clinical trials. Our Chairs for the column are Dr. Daniel Sargent and Dr. Qian Shi, Division of Biomedical Statistics and Informatics, Mayo Clinic, Rochester, MN, USA. The column is expected to convey statistical knowledge which is essential to trial design, conduct, and monitoring for a wide range of researchers in the oncology area. Through illustrations of the basic concepts, discussions of current debates and concerns in the literature, and highlights of evolutionary new developments, we are hoping to engage and strengthen the collaboration between statisticians and oncologists for conducting innovative clinical trials. Please follow the column and enjoy.
Introduction
Clinical trials are prospective intervention studies with human participants to investigate experimental drugs under rigorously specified conditions. A well designed and conducted clinical trial is the most definitive method for assessing the treatment effect of new drugs and has become an integral part of drug development (1,2).
The cost of drug development has substantially increased in the past several decades. However, escalating costs have not translated to greater success rates in such clinical trials, nor to a proportional increase in the number of approved drugs. For example, as recorded by BioMedTracker, for 4,275 clinical trials that released their results from 2003 to 2010, the overall success rate for final approval of the trial drug or intervention was only 9% (3). Factors that influence this low success rate may include a diminished margin for health improvement; a current limit to the use of genomics and other new biological science and technology; a decreased number of research companies because of mergers and other business arrangements; and the increasing complexity of bringing potential experimental therapies to trial (4). To address these issues, in 2006, the United States Food and Drug Administration (FDA) released a critical path opportunities list (5) that called for further development and use of innovative designs that apply the information accumulating in the trial to guide the trial as it moves forward. Specifically, the FDA began encouraging the use of adaptive design methods in clinical trials.
An adaptive design differs from a traditional design in that it uses accumulating data from the ongoing trial to modify certain aspects of the study (6). In general, an adaptive design may allow for adaptive dose escalation/de-escalation; early stopping of the trial for toxicity, efficacy or futility; dropping or adding new treatment arms; using a seamless phase transition; adjusting an adaptive randomization scheme based on patient response or covariates; sample size re-estimation; and biomarker-guided treatment allocation (7,8). The purpose of the adaptive design is to give the investigator the flexibility to identify the best clinical benefit of the treatment as the trial progresses and then use that information to provide the best treatment to patients newly enrolling in the trial without undermining the scientific validity and integrity of the intended trial.
As the trial progresses and data accrue, the adaptive deign continuously learns the toxicity and efficacy profiles of the experimental drugs and uses that accumulating information to guide and modify the ongoing trial. The motto for the adaptive design is “We learn as we go”. As a result, the adaptive design has potential advantages of improving the study power, reducing the sample size and total cost, treating more patients with more effective treatments, correctly identifying efficacious drugs for specific subgroups of patients based on their biomarker profiles, and shortening the time for drug development. Because of these potential advantages, the interest in adaptive designs has risen. Many, but not all adaptive designs are formulated under the Bayesian framework. Bayesian methods model the parameter of interest by (I) obtaining the prior distribution; (II) collecting data to calculate the data likelihood; and then (III) computing the posterior distribution using Bayes theorem. The Bayesian method is adaptive in nature and provides an ideal statistical framework for adaptive trial designs (9). Numerous publications on this topic are available in the literature, and adaptive clinical trial designs are being used increasingly in many areas of research (10-12). Indeed, academic journals have published special sections or issues on the topic of adaptive designs (e.g., Biometrics, Statistics in Medicine, the Journal of Biopharmaceutical Statistics, Statistics in Bioscience, and others) (6). The pharmaceutical industry and regulatory agencies have also found adaptive designs attractive because of their potential advantages and because they reflect medical practice in the real world. For example, several organizations have established adaptive design working groups, which have proposed strategies, methodologies, and implementation policies for consideration by regulatory agencies. These include the Pharmaceutical Research and Manufacturers of America (PhRMA), Biotechnology Industry Organization (BIO), the Biopharmaceutical section of the American Statistical Association, and the Drug Information Association (DIA). The Center for Biologics Evaluation and Research and the Center for Drug Evaluation and Research at the FDA have jointly issued a guidance document for planning and implementing adaptive designs in clinical trials (13).
The purpose of this article is to review the methodology, development, and implementation of adaptive designs in clinical research. This paper is organized as follows. We introduce adaptive design methods commonly employed in clinical trials, which include adaptive dose-finding methods, interim analysis, adaptive randomization, biomarker-guided randomization, and seamless designs. Then, we present two recently conducted clinical trials that utilized adaptive designs. Finally, we discuss practical issues encountered in the implementation of adaptive clinical trial designs.
Adaptive dose-finding design
A phase I clinical trial typically assesses the safety of a new drug, with the primary aim of determining the maximum tolerated does (MTD), which is defined as the dose that has a toxicity probability closest to the targeted toxicity rate specified by the investigators. Broadly speaking, phase I dose-finding designs can be classified into two categories: the algorithm-based up-and-down design, and the model-based adaptive design.
The up-and-down design typically uses an algorithm-based approach that does not include assumption modeling, and follows strict, pre-specified rules in the dose-finding procedure. Examples of the up-and-down design include the “3+3” design (14) and the accelerated titration design (15). In contrast to the algorithm-based up-and-down design, the model-based adaptive design uses the accumulating data to estimate the dose-toxicity curve and guides the dose escalation or de-escalation as the trial moves along; hence, it is more flexible and efficient. The commonly used model-based design includes, but is not limit to the continual reassessment method (CRM) (16-18), the Bayesian model averaging continual reassessment method (BMA-CRM) (19), the escalation with overdose control (EWOC) design (20). In addition, several model-based dose-finding designs have been proposed for trial with late-onset toxicity (e.g., TITE-CRM and EM-CRM) (21-23), phase I/II trial (24-28) and drug-drug combination trial (29-33). Recently, Braun (34) provided a comprehensive review for the adaptive phase I dose-finding design.
Interim analysis
After the phase I trial, a phase II trial is conducted to evaluate the drugs’ therapeutic effects at the recommended dose. The efficacy outcome in a phase II trial is often a short-term, binary endpoint. When a new treatment shows promising efficacy, a phase III trial usually follows, with a longer-term, time-to-event outcome as a confirmatory assessment. The one-stage design performs only one final analysis at the end of the trial. Although the one-stage design is easy to plan and implement, it lacks flexibility and efficiency. In contrast, the sequential design uses the accumulated data to perform an interim analysis in the middle of the trial and then can use those results to adaptively change the plan of the trial.
Gehan’s two-stage design (35) and Simon’s two-stage design (36) have been proposed as sequential designs for a single-arm phase II study. The purpose of the single-arm trial is to test whether the efficacy rate of a new treatment is better than that of the standard treatment based on historical data. The trial design reaches a pre-specified target rate by controlling the type I and type II error rates.
For a two-arm trial in which an experimental treatment is compared with a standard treatment to assess the therapeutic effect, the group sequential design can be used to minimize the total number of patients enrolled in the trial. This design stops the trial early if the interim data show either overwhelming evidence of a strong treatment difference or the clear absence of a treatment difference. Consequently, this design allows for more timely adjustments to be made in the drug developmental process. Specifically, Pocock (37) and O’Brien and Fleming (38) proposed two kinds of group sequential designs with different stopping boundaries. The former design uses equal probability stopping boundaries throughout the trial; the latter uses more stringent probability stopping boundaries at the beginning of the trial, with more lenient boundaries toward the end of the trial. Wang and Tsiatis (39) generalized the result and proposed group sequential designs that incorporate both Pocock’s design and O’Brien and Fleming’s design as special cases. DeMets and Lan (40) proposed the alpha-spending function approach as a more flexible version of the group sequential design. Instead of a fixed number of interim analyses, the alpha-spending function uses the accumulated type I error rate at the repeated interim analyses to determine the stopping boundaries during the trial. One main goal of all the group sequential trials is to control the overall type I error while performing multiple significance testing. Jennison and Turnbull provide further discussion of group sequential designs (41).
Although the group sequential design may terminate the trial earlier, the maximum sample size of this design is usually fixed. Traditionally, the fixed sample size is derived based on a pre-specified power to detect a clinically meaningful treatment difference expressed as the effect size. The effect size is typically elicited from external historical data when the trial is designed. However, due to different study conditions and sampling bias, historical data may not provide an accurate estimate of the effect size for the current trial. Consequently, the sample size for the ongoing trial may be overestimated and thus waste resources, or underestimated and thus result in an under-powered study. To overcome such an unforeseen deficiency, several adaptive designs have been proposed that re-estimate the sample size based on the data that accrue during the trial. For example, Proschan and Hunsberger (42) proposed a two-stage design with sample size re-estimation after stage 1. This design allows for the termination of the trial in stage 1 and determines each stopping boundary and critical value in the two stages according to Fisher’s combination criterion to preserve the overall type I error. The design uses stage 1 data to estimate the effect size, based on which it then re-estimates the sample size for stage 2. The sample size in stage 2 is selected to satisfy a pre-specified conditional power, which is defined as the probability of rejecting the null hypothesis based on the observed data in stage 1. The self-designing strategy is another adaptive sample size re-estimation design (43). This design uses the accumulating data to automatically decide whether to stop the trial due to futility or expand the trial to achieve the desirable power. This design also does not require the pre-determination of the maximum sample size and can maintain the overall type I error rate. The adaptive design with sample size re-estimation appears attractive; however, as pointed out by Tsiatis and Mehta (44), the design is inefficient in the sense that it can always be uniformly improved by a standard group sequential design based on the sequentially computed likelihood ratio test. Hence, additional caution and further study are needed before designing studies with sample size re-estimation.
Multiplicity may arise when several repeated hypotheses are tested during a trial. As a result, Frequentist adaptive designs make great efforts to maintain the type I error rate under the nominal level. In contrast, the Bayesian approach is more flexible, as early stopping does not affect Bayesian inference. Under the Bayesian framework, the posterior distribution continues to be updated by synthesizing the prior information and the updated data. We learn as we go. Hence, it is natural and appealing to consider an interim analysis under the Bayesian framework. Considering the response outcome as binary, Thall and Simon (45) proposed a practical guideline for implementing a phase II Bayesian adaptive design based on the posterior probability. Specifically, they first assign a non-informative beta prior distribution for the experimental arm and an informative prior for the standard treatment effect. Then, after treating each new cohort of patients, the posterior distribution of the treatment effect can be easily calculated from a conjugate beta distribution. After that, the posterior probability that the experimental treatment effect exceeds the standard treatment effect by at least a clinically meaningful margin is computed and used to define the early stopping rule. If this probability is larger than an upper boundary, the trial is stopped early for efficacy and the experimental treatment is claimed as promising. Alternatively, if this probability is less than a lower boundary, the trial is terminated for futility and the experimental treatment is claimed as non-promising. Otherwise, the trial continues to treat more patients. If the trial reaches the maximum sample size, a final hypothesis testing is carried out to assess the therapeutic effect of the experimental treatment. The stopping boundaries are calibrated according to simulations to maintain desirable operating characteristics, including the control of type I and type II errors. Thall et al. (46) further extended this idea by jointly modeling the bivariate outcomes of both efficacy and toxicity with a conjugate Dirichlet distribution. The stopping rule can be determined similarly. Because the toxicity outcome is also monitored, the trial can be terminated for toxicity if the posterior probability of toxicity is large during the interim analysis. In addition to the binary trial, a similar Bayesian adaptive design has been investigated for a survival trial in which the response outcome is time-to-event (47).
A related trial design that uses the Bayesian framework is the predictive probability design. For this design, we consider the posterior distribution, which characterizes the distribution of the model parameter based on the observed data, and the posterior predictive distribution, which characterizes the distribution of the future data conditioned on the observed data but projected into the future. Under the Bayesian framework, the posterior predictive distribution can be derived by averaging the distribution of the unobserved data over the model parameter space given the observed data. Applying this posterior predictive distribution, Lee and Liu (48) developed a predictive probability that represents the future trial conclusion based on the strength of the currently observed data. They use this predictive probability for decision making at each interim analysis during the trial. Stopping boundaries for futility are constructed accordingly. The predictive probability design allows for continuous monitoring of the trial. It is more flexible and efficient than the fixed, multi-stage design.
Adaptive randomization
When multiple treatment arms are investigated in a clinical trial, randomization is needed to ensure there is an objective comparison of the different treatment groups. The primary goal of randomization is to balance different treatment groups with respect to all the known and unknown prognostic factors, thereby obtaining a credible and unbiased result. To achieve this goal, equal randomization (1:1) or randomization with a fixed ratio (e.g., 2:1) among the different treatments are the most commonly used randomization schemes. In addition, several adaptive randomization schemes that allow the allocation ratio for each arm to change as the trial continues have been proposed. Based on different objectives, adaptive randomization designs can be classified as baseline covariate-adaptive randomization or response-adaptive randomization. The former design intends to balance the prognostic factors among the treatment arms, while the latter aims to allocate more patients to the better treatment arm.
Pocock and Simon (49) proposed the minimization method for covariate-adaptive randomization. This method determines the treatment allocation for the next enrolling patient based on the overall covariate distribution among the treatment groups in order to achieve a desirable balance of the corresponding properties. Efron (50) developed the biased coin design for a two-arm randomized trial to balance the number of patients allocated to the different arms. This design tosses a coin that is biased with a probability of landing on its head to determine the allocation ratio. The design imposes the ability to achieve balance among the different arms. For response-adaptive randomization, Zelen (51) proposed the play-the-winner rule for the randomization of patients in a two-arm trial. In that design, the next enrolling patient's allocation depends solely on the previous patient's response to treatment. If the previous patient had a successful response, the next patient will be assigned to the same treatment. Otherwise, the next patient will be assigned to the alternative treatment. This deterministic scheme was further modified by a randomized play-the-winner scheme (52).
In response-adaptive randomization schemes, the randomization ratio can be specified to optimize certain criteria. For example, the Neyman allocation assigns patients on a basis that is proportional to the squared root of the variance of the parameter in order to maximize the statistical power of the test. Rosenberger et al. (53) proposed an optimal design that minimizes the expected number of non-responders while fixing the variance of the test statistic. However, these optimal randomization ratios often depend on the design parameters, which are generally unknown at the beginning of a trial. Hence, response-adaptive randomization needs to use interim data to estimate these parameters and then adjust the randomization ratios accordingly by incorporating the bias and variability of the randomization procedure to achieve certain optimal properties. One such design is the doubly adaptive biased coin design (54,55). This design allows the randomization ratio to be changed adaptively depending on both the observed allocation proportion and the estimated target allocation ratio. Consequently, this design simultaneously balances the target allocation ratio and the current estimation according to a pre-specified allocation function. As the trial continues, the randomization ratio converges to the target ratio to ensure the optimality of the design.
Bayesian adaptive randomization designs use the posterior distribution of the treatment effect to construct the randomization ratio (56). Before conducting the adaptive randomization, the investigators can choose to use an equal randomization phase at the beginning of the trial to gather information on treatment efficacy. Subsequently, they can calculate the posterior probability that each treatment has the highest therapeutic effect. Then, the next new patient can be randomized to a treatment with a randomization probability that is proportional to the associated posterior probability. The power transformation can be incorporated to control the degree of imbalance of the randomization scheme. For example, if this parameter equals 0, then the adaptive randomization reduces to equal randomization; if this value equals infinity, the adaptive randomization becomes the deterministic play-the-winner rule. Notice that using the posterior probability of the treatment effect is not the only way to construct the randomization ratio. For example, Lee et al. (57) proposed to construct the randomization ratio based on the posterior mean of the treatment effect. In addition, as illustrated in Figure 1, a Bayesian adaptive clinical trial design often incorporates both the adaptive randomization scheme and early stopping rule to conduct the trial. For example, Yin et al. (58) developed a Bayesian phase II clinical trial design with adaptive randomization and predictive probability. That design uses adaptive randomization to assign more patients to the more efficacious treatment arm. Meanwhile, the trial is continuously monitored using the predictive probability and can be terminated early due to efficacy or futility.
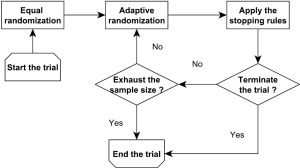
In general, equal randomization can improve the efficiency of a trial by maximizing the statistical power. It also enhances the group ethics of a trial, which benefit the overall relevant population. On the other hand, adaptive randomization offers a higher probability of assigning more patients to the more efficacious treatment, and therefore enhances the individual ethics of the trial, which benefit the patients enrolled in the trial. There are different opinions regarding which randomization scheme is the best choice for guiding a clinical trial. Korn and Freidlin (59) conducted a simulation study to compare equal randomization with adaptive randomization for a two-arm trial with a binary endpoint. They concluded that equal randomization should be used because the improvement in individual ethics that is achieved with adaptive randomization is limited, especially when one considers the additional complexity of implementing the adaptive randomization scheme in a trial. Lee et al. (60) conducted extensive simulation studies to investigate this issue and concluded that when the difference between the treatments under investigation is large, adaptive randomization outperforms equal randomization in both statistical power and the overall response rate, but the difference diminishes quickly when the early stopping rule is added. Adaptive randomization also outperforms equal randomization when the proportion of patients outside the trial is small, e.g., when applied to rare diseases. Hence, they recommended using adaptive randomization when the treatment difference is large or the relevant disease is rare. Berry et al. (61) claimed that although the benefit of implementing adaptive randomization is limited for two-arm trials, the improvement should be significant for multi-arm trials. Similar results were also reported by Wason and Trippa (62). They compared Bayesian adaptive randomization with the multi-arm, multi-stage (MAMS) designs. They suggested that when at least one treatment arm is much more effective than the others, the adaptive randomization design is more efficient than the equal randomization designs.
Seamless design
Cancer clinical trials are traditionally conducted in different phases. A phase I trial identifies the MTD of the new drug based on the toxicity outcomes. Subsequently, a separate phase II trial is carried out to examine the efficacy of the drug at the identified MTD. Then, a randomized phase III trial is conducted to compare the experimental therapy with the standard therapy. To streamline the drug development process and reduce the associated time and cost, there is a growing trend to integrate different response outcomes and phases into one clinical trial (63-66). To incorporate both toxicity and efficacy outcomes, Thall and Cook (24) proposed a dose-finding design based on the efficacy-toxicity trade-off. Considering both efficacy and toxicity outcomes as time-to-event data, Yuan and Yin (25) proposed another Bayesian adaptive design that linked the toxicity and efficacy distributions by the Clayton copula. Zang et al. (26) recently proposed three adaptive dose-finding designs for trials that evaluate molecularly targeted agents, for which the dose-response curves are unimodal or plateaued. The first proposed design is parametric and assumes a logistic dose-efficacy curve for dose finding; the second design is nonparametric and uses the isotonic regression to identify the optimal biological dose; and the third design has the spirit of a “semi-parametric” approach by assuming a logistic model only locally around the current dose. Based on the simulation results, the authors recommend the nonparametric and semi-parametric designs. Other related adaptive designs include the trinomial CRM design (27) and the two-stage design (28).
To integrate phase I and phase II stages, Huang et al. (67) proposed a seamless phase I/II design that evaluates both the toxicity and efficacy of drug combinations in one trial. The first stage (phase I) uses the “3+3” approach to conduct the dose-finding procedure based on toxicity, with the objective of finding the admissible dose set. This dose set is then forwarded to the second stage (phase II) to assess efficacy, which involves adaptive randomization of patients to the admissible dose combinations based on Bayesian posterior probabilities. A Bayesian early stopping rule is added to the second stage for possible early termination of the trial due to safety concerns, efficacy or futility. At the end of the trial, the most efficacious drug combination in the admissible set is selected. This design is seamless in the sense that both the toxicity and efficacy outcomes are collected throughout the trial and are used for the ongoing adaptive dose finding and randomization, with the possibility of early stopping. Yuan and Yin (68) developed another seamless phase I/II design for identifying the most efficacious dose combination that satisfies certain safety requirements for drug combination trials. They employ a copula model to identify the admissible dose set based on toxicity in the first stage of the trial. The second stage uses a novel adaptive randomization procedure that is based on a moving reference to compare the relative efficacy among the treatments under investigation. Hoering et al. (69) proposed a seamless phase I/II trial design for assessing the toxicity and efficacy of targeted agents. The first stage uses a traditional dose-finding approach that assesses toxicity to find the MTD. For the second stage of the trial, they propose using a modified phase II selection design for 2 or 3 dose levels at and below the MTD, and evaluating the efficacy and toxicity at each dose level.
Phase II cancer trials generally investigate the tumor response. If a phase II trial shows a favorable tumor shrinkage response, then a confirmatory phase III trial follows to determine the efficacy of the new treatment based on a longer-term endpoint such as the patients’ length of survival. Both phase II and phase III trials can be time-consuming. Generally speaking, a phase II trial has a duration of more than 18 months, while a phase III trial is ongoing for at least another 2 years after that (10). This does not include the “white space”, i.e., the time between these two trial phases that is required for analyzing the phase II data and determining the design of the phase III study. To hasten drug development and improve the success rate at the same time, a seamless phase II/III trial design has been proposed. This design combines the learning and confirmatory stages into one trial. A seamless phase II/III trial is typically conducted using multiple drugs and multiple dose levels of the experimental drug. For the learning stage (phase II), the most efficacious dose among the multiple doses of the experimental drug is selected and seamlessly forwarded to the confirmatory stage (phase III). Under this design, a smaller confirmatory study can be conducted to compare the improvement in survival time between patients who are administered the most efficacious dose of the experimental drug and those who are given the control drug.
Depending on whether the patients in the learning stage (phase II) are counted, a seamless phase II/III design can be classified as an inferentially seamless design or an operationally seamless design (11). In the inferentially seamless design, the data from patients in the learning stage who share the same treatments and have the same primary endpoint as their counterparts in the confirmatory stage are included in the final analysis of the trial. Consequently, the inferentially seamless design can result in a higher overall success rate because the early positive results are included in the final analysis. Thus, a potential bias may arise because the information from the learning stage is used for both conducting and analyzing the confirmatory stage of the trial. Calibration simulations are needed in the final analysis to adjust for the potential inflation of the overall type I error rate. In the operationally seamless design, the results of the two stages are analyzed separately. Hence, this design has no impact on the type I error rate of the confirmatory stage of the trial. Because there is no “white space” between the learning and confirmatory stages (phases II and III), the operationally seamless design streamlines the overall trial. For example, Inoue et al. (70) compared the seamless design with separate designs that have the same operating characteristics and found that the adoption of the seamless design can result in an average 30% to 50% sample size reduction as well as a significantly shortened total duration of the trial.
Several seamless phase II/III designs have been proposed in the literature. Huang et al. (71) proposed a seamless phase II/III design when short-term tumor response information is available in the learning stage. They use a Bayesian model to connect the short-term response with the long-term survival time such that the adaptive randomization procedure based on the survival endpoint can be sped up by incorporating the response information. Interim monitoring is conducted during the trial and the final inference is made based on the primary survival response. Stallard (72) investigated a seamless phase II/III trial that selected the most promising experimental treatments at the interim analysis. If the short-term data are available for some patients for whom the primary endpoints are not available, this design uses the short-term endpoints at the interim analysis to adjust group-sequential boundaries to control the type I error rates. Kimani et al. (73) proposed an adaptive two-stage design for trials in which the experimental treatments are different dose levels of the same drug. The dose selection at the end of the first stage is made by comparing the predictive power of the admissible sets of doses. Bischoff and Miller (74) provided the sample size formula of an adaptive two-stage design for the seamless phase II/III trial.
When several new treatments are compared with a control treatment within a multi-arm trial, the MAMS design (62,75) has been proposed to collect the data of the different treatments. The purpose of the MAMS design is to identify the most promising treatment and assign more patients to that treatment. The MAMS design also uses the interim data to conduct the trial. But, unlike adaptive randomization, the MAMS design does not change the allocation probability for each treatment. The experimental treatments that cross the pre-specified stopping boundaries are dropped from the MAMS trial. The MAMS design has been applied in several real trials, including STAMPEDE and TALLOR (76).
Biomarker-guided adaptive design
Thanks to an improved understanding of cancer biology and rapid advancements in biomedicine, we have entered the era of targeted therapies in clinical oncology (77). Targeted cancer therapies are often expected to be more effective and less harmful than other types of therapies, such as chemotherapy and radiotherapy (78). The clinical application of a targeted therapy requires the identification of biomarkers that can be used to identify patients who are likely to be sensitive to the targeted therapy (79-82).
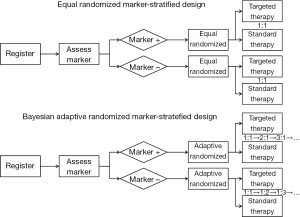
Recently, several biomarker-guided adaptive designs have been proposed to identify, validate and utilize biomarkers in clinical trials. These trial designs include the marker-stratified design, marker-strategy design (83-85), enrichment design (86-89), basket design (90), N-of-1 design (91) and master protocol design (92). The marker-stratified design typically uses equal randomization to allocate patients to different treatment arms. Alternatively, Lee et al. (57) proposed a Bayesian adaptive marker-stratified design. This design uses Bayesian response-adaptive randomization to provide more patients with more effective treatments according to the patients’ biomarker profiles. In addition, an interim analysis with early stopping rules is implemented to increase the efficiency of the designs. Figure 2 provides flowcharts of the equal randomized marker-stratified design and the Bayesian adaptive randomized mark-stratified design. For a comprehensive review of the biomarker-guided design, one can refer to the review article written by Simon (93).
Trial examples
We introduce two recently conducted high-profile, large-scale randomized phase II clinical trials that utilize adaptive designs: the “Biomarker-integrated approaches of targeted therapy of lung cancer elimination” (BATTLE) trial and the “Investigation of serial studies to predict your therapeutic response with imaging and molecular analysis” (ISPY-2) trial. Both trials have implemented adaptive randomization schemes to assign patients to the more efficacious treatments based on their biomarker-guided profiles, and use interim analyses to monitor the efficacy outcomes during the trial.
The BATTLE trial (94,95) enrolled patients with stage IV recurrent non-small cell lung cancer. The primary endpoint was the eight-week disease control rate, which was recorded as a binary outcome. The four biomarker profiles used in the trial were EGFR mutation/amplification, KRAS and BRAF mutation, VEGF and VEGFR expressions, and Cyclin D1/RXR expressions. Four targeted therapies, erlotinib, vandetanib, erlotinib plus bexarotene, and sorafenib, were evaluated, with one therapy targeting each one of the four biomarker profiles. The goals of the trial were to test the treatment efficacy and biomarker effect, and to evaluate their predictive roles in providing better treatment to patients in the trial based on their biomarker profiles. The trial used Bayesian methods to model the treatment-response relationship and used a hierarchical probit model to borrow strength across the different biomarker subgroups. It used an adaptive randomization scheme to allocate patients to the different treatments; hence, patients had higher probabilities of being assigned to better treatments based on their biomarker profiles. Also, the early stopping rule for futility was equipped to drop the potentially inferior treatments from the options available for newly enrolling patients who had certain biomarker profiles. The BATTLE trial enrolled 341 patients and randomized 255 of them under the proposed adaptive randomization scheme. The overall results included a 46% 8-week disease control rate, confirmed the pre-specified hypotheses, and showed a positive benefit from sorafenib among patients with mutant KRAS profiles (95).
Based on the findings of the BATTLE trial, a follow-up BATTLE-2 trial was started, and is ongoing (96). The BATTLE-2 trial evaluates four treatment regimens, erlotinib, sorafenib, erlotinib + MK2206, and MK2206 + AZD6244, in a two-stage design with adaptive randomization. Each of the two stages will enroll 200 patients. Biomarker selection is conducted in 3 steps: training, testing and validation. In the training step, 10-15 potential prognostic and predictive markers are selected from the previous BATTLE experience, cell line data, and relevant information published in the literature. The selection of these markers is based on the pre-BATTLE-2 information. In the testing step, the selected markers are tested using the data acquired from stage 1 of the BATTLE-2 trial. The expectation is to select no more than five significant markers using the statistical two-step LASSO method. In the validation step, the markers selected in the first stage of the BATTLE-2 trial are used for adaptive randomization in the second stage of BATTLE-2, and their prognostic and/or predictive values will be validated.
The ISPY-2 trial (97) is a multicenter phase II trial in the neoadjuvant setting for patients with breast cancer. The primary end point is pathologic complete response (PCR) at the time of surgery. The tumor burden assessed by MRI during treatment serves as an auxiliary marker to predict the treatment effect of PCR. The patient population is partitioned into ten subgroups depending on hormone-receptor (HR) status, HER2 status and Mamma Print signature. All patients receive standard chemotherapy for breast cancer in the neoadjuvant setting: 12 weeks of taxane administration and four biweekly or triweekly cycles of an anthracycline (doxorubicin) plus cyclophosphamide. Experimental drugs are added to the taxane cycle of treatment. The overall goal of the trial is to prospectively learn as efficiently as possible which patients respond to each experimental treatment based on their biomarker profiles. Adaptive randomization with interim analysis is used within each biomarker subgroup, with the treatments that are performing better within a subgroup being assigned with greater probability to patients belonging to that subgroup. In addition, the trial may be terminated early for futility or efficacy. The phase II drug-screening stage is followed by a phase III confirmatory stage. The drug recommendation for the phase III stage is based on a predictive probability of each drug being successful in a 300-patient phase III trial. The trial will screen 12 different drugs. The FDA is allowing for adaptive flexibility in the trial: the investigators can graduate a successful drug from the trial, drop an unsuccessful drug from the trial, or add a new drug during the trial rather than initiating a new protocol, which will save a considerable amount of time (98). The ISPY-2 trial has recently shown that when added to standard, pre-surgery chemotherapy, the combination of carboplatin and the molecularly targeted experimental drug veliparib improve the rate of tumor response in women with triple-negative breast cancer. In addition, based on a high probability of success in the phase III stage for women with HER2-positive/HR-negative disease status, the ISPY-2 trial has graduated another experimental drug, neratinib, from the trial. These two drug graduations serve as important evidence of the potential of the ISPY-2 trial design to significantly reduce the cost of drug development and speed the process of screening drugs, with the goal of bringing safe and effective new drugs to market more efficiently (99).
Discussion
Adaptive clinical trial designs hold great promise for improving the flexibility and efficiency of clinical trial conduct. They can efficiently identify effective drugs and eliminate ineffective drugs from further consideration, test and validate biomarkers, match effective treatments with specific subgroups of patients based on their biomarker profiles, reduce the overall sample size, and shorten the time required for drug development. However, adaptive trial designs are more complicated than traditional designs and demand more attention throughout the study design process and the trial conduct. The operating characteristics of the adaptive trial design need to be explicitly examined under a spectrum of plausible conditions. Frequently conducting interim analyses brings the added pressure of requiring timely data collection and computation. The collaborating statisticians should be more closely involved in monitoring the trial conduct to make appropriate decisions based on the interim data. Also, the application of adaptive designs requires new software and tools for monitoring the statistical design of the trial, analyzing the data, and reporting the results (100). A list of statistical software that can be used to design and conduct various phases of adaptive clinical trials (and access to that software) is available at https://biostatistics.mdanderson.org/SoftwareDownload/.
The characteristics of patients who enroll in a given trial may change substantially over the course of the randomized trial because randomization tends to favor a more effective experimental drug, especially in an unblinded trial (59). Such a trend within the trial population can lead to a biased comparison of the treatments under investigation. Because adaptive designs use the accumulating response data to guide the trial conduct, they are more sensitive to such a population drift. If the patient population changes dramatically during the time period of the trial, then an adaptive design may not be appropriate and regression analysis can be used to adjust the potential impact of the population drift.
Another practical concern for adaptive trial designs is the security of the information collected during the trial (101). Adaptations that occur during the trial and which become known to anyone other than the members of the Data and Safety Monitoring Board (DSMB), who strictly maintain the confidentiality of trial data, may seriously affect the ethics and integrity of the trial. For example, an increase in the sample size following an interim analysis may be interpreted as a sign that the expected treatment effect is not present. This may then impact the actions of any investigator involved in the trial. The possibility of information leakage may not be an issue in a short-term phase II trial, but can limit the credibility of an unblinded phase III trial.
Last, but not least, the logistics of the adaptive design is more complicated than those of the conventional trial design (102). Adaptive trial designs require a central database in which to store all the outcome data. This database must be connected to the software that determines treatment assignments or other adaptive aspects of the trial such as interim monitoring and the evaluation of the stopping rules. An integrated database with a web-based interface is particularly useful for conducting multi-center adaptive trials. Timely and accurate data collection is critically important to the success of adaptive trials.
To summarize, well planned and carefully conducted clinical trials that use adaptive designs have the potential to improve drug development, provide greater benefit to the enrolled patients, and effectively address many research questions of interest. However, an adaptive trial design is not a panacea, nor is it a remedy for bad planning. Designing and implementing an adaptive trial design requires specialized learning and specialized software. We need time to translate theoretical developments in statistical trial design to practice. Guidance from regulatory agencies (e.g., the FDA) and industry support are also important. The risk associated with adaptive trial designs must be assessed within the context of the potential gains. The objective of the clinical trial must first be clearly established and evaluated before determining whether the adaptive design will have advantages over the alternative conventional designs. The operating characteristics of the potential adaptive design must be investigated through extensive simulations and calibrations. In addition, we must keep in mind that no adaptive design is without limitations, but it can offer a timely and informative "learn as we go" approach. Adaptive designs have the ability to improve their performance as the trial continues. We should not be discouraged by the complexity or practical requirements of adaptive designs as they are readily addressable, particularly, with the improved clinical trial infrastructure. Adaptive designs are promising and have much to offer. We encourage continued learning and improvement through the implementation of adaptive trial designs so that we can turn promise into progress.
Acknowledgements
This work was supported in part by the grant CA016672 from the United States National Cancer Institute. The authors thank Lee Ann Chastain for her editorial assistance.
Disclosure: The authors declare no conflicts of interest.
References
- Pocock SJ. eds. Clinical trials: a practical approach. Chichester: Wiley, 1983.
- Piantadosi S. eds. Clinical trials: a methodologic perspective. Hoboken: Wiley-Interscience, 2005.
- Bio/BioMedTracker. Clinical Trial Success Rates Study, 2011. Available online: http://insidebioia.files.wordpress.com/2011/02/bio-ceo-biomedtracker-bio-study-handout-final-2-15-2011.pdf
- Woodcock J. FDA introduction comments: clinical studies design and evaluation issues. Clinical trials 2005;2:273-5. [PubMed]
- U.S. Food and Drug Administration. Critical Path Opportunities List, 2006. Available online: http://www.fda.gov/downloads/scienceresearch/specialtopics/criticalpathinitiative/criticalpathopportunitiesreports/UCM077258.pdf
- Gallo P, Chuang S, Dragalin V, et al. Executive summary of the PhRMA working group on adaptive designs in clinical drug development. J Biopharm Stat 2006;16:275-83. [PubMed]
- Berry DA. Bayesian clinical trials. Nat Rev Drug Discov 2006;5:27-36. [PubMed]
- Chow SC, Chang M. eds. Adaptive design methods in clinical trials. City: Chapman/ & Hall/CRC, 2006.
- Lee JJ, Chu CT. Bayesian clinical trials in action. Stat Med 2012;31:2955-72. [PubMed]
- Berry SM, Carlin BP, Lee JJ, et al. eds. Bayesian adaptive methods for clinical trials. Boca Raton, FL: Chapman and Hall/CRC, 2010.
- Berry DA. Adaptive clinical trials in oncology. Nat Rev Clin Oncol 2011;9:199-207. [PubMed]
- Ying G. eds. Clinical trial design: Bayesian and frequentist adaptive methods. New Jersey: Wiley, 2012.
- FDA Guidance for industry: Adaptive design clinical trials for drugs and biologics. U.S. Department of Health and Human Services, Food and Drug Administration (CDER/CBER). Available online: http://www.fda.gov/downloads/DrugsGuidanceComplianceRegulatoryInformation/Guidances/UCM201790.pdf
- Storer BE. Design and analysis of Phase I clinical trials. Biometrics 1989;45:925-37. [PubMed]
- Simon R, Freidlin B, Rubinstein L, et al. Accelerated titration designs for phase I clinical trials in oncology. Journal of the National Cancer Institute 1997;89:1138-47. [PubMed]
- O'Quigley J, Pepe M, Fisher LD. Continual reassessment method: A practical design for phase I clinical trials in cancer. Biometrics 1990;46:33-48. [PubMed]
- Faries D. Practical modification of the continual reassessment methods for phase I clinical trials. J Biopharm Stat 1994;4:147-64. [PubMed]
- Goodman SN, Zahurak ML, Piantadosi S. Some practical improvements in the continual reassessment methods to phase I studies. Stat Med 1995;14:1149-61. [PubMed]
- Yin G, Yuan Y. Bayesian model averaging continual reassessment method in phase I clinical trials. J Am Stat Assoc 2009;104:954-68.
- Babb J, Rogatko A, Zacks S. Cancer phase I clinical trials: Efficient dose escalation with overdose control. Stat Med 1998;17:1103-20. [PubMed]
- Cheung YK, Chappell R. Sequential designs for phase I clinical trials with late-onset toxicities. Biometrics 2000;56:1177-82. [PubMed]
- Yuan Y, Yin G. Robust EM continual reassessment method in oncology dose finding. J Am Stat Assoc 2011;106:818-31. [PubMed]
- Liu S, Yin G, Yuan Y. Bayesian data augmentation dose finding with continual reassessment method and delayed toxicity. Ann Appl Stat 2013;7:1837-2457. [PubMed]
- Thall PF, Cook J. Dose-finding based on efficacy-toxicity trade-off. Biometrics 2004;60:684-93. [PubMed]
- Yuan Y, Yin G. Bayesian dose finding by jointly modeling toxicity and efficacy as time-to-event outcomes. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2009;58:719-36.
- Zang Y, Lee JJ, Yuan Y. Adaptive designs for identifying optimal biological dose for molecularly targeted agents. Clin Trials 2014;11:319-27. [PubMed]
- Zhang W, Sargent DJ, Mandrekar SJ. An adaptive dose-finding design incorporating both toxicity and efficacy. Stat Med 2006;25:2365-83. [PubMed]
- Polley MY, Cheung YK. Two-stage designs for dose-finding trials with a biologic endpoint using stepwise tests. Biometrics 2008;64:232-41. [PubMed]
- Thall PF, Millikan R, Muller P, et al. Dose-finding with two agents in phase I oncology trials. Biometrics 2003;59:487-96. [PubMed]
- Yin G, Yuan Y. Bayesian dose-finding in oncology for drug combination by coupla regression. Journal of the Royal Statistical Society, Series C 2009;58:211-24.
- Yuan Y, Yin G. Sequential continual reassessment method for two-dimensional dose findings. Stat Med 2008;27:5664-78. [PubMed]
- Yin G, Yuan Y. A latent contingency table approach to dose-finding for combinations of two agents. Biometrics 2009;65:866-75. [PubMed]
- Mandrekar SJ, Cui Y, Sargent DJ. An adaptive phase I design for identifying a biologically optimal dose for dual agent drug combinations. Stat Med 2007;26:2317-30. [PubMed]
- Braun TM. The current design of oncology phase I clinical trials: progressing from algorithms to statistical models. Chin Clin Oncol 2014;3:2.
- Gehan EA. The determination of the number of patients required in a follow-up trial of a new chemotherapeutic agent. J Chronic Dis 1961;13:346-53. [PubMed]
- Simon R. Optimal two-stage designs for phase II clinical trials. Control Clin Trials 1989;10:1-10. [PubMed]
- Pocock SJ. Group sequential method in the design and analysis of clinical trials. Biometrika 1977;64:191-9.
- O'Brien PC, Fleming TR. A multiple testing procedure for clinical trials. Biometrics 1979;35:549-56. [PubMed]
- Wang SK, Tsiatis AA. Approximately optimal one-parameter boundaries for group sequential trials. Biometrics 1987;43:193-9. [PubMed]
- DeMets DL, Lan KK. Interim analyses: the alpha spending function approach. Stat Med 1994;13:1341-52. [PubMed]
- Jennison C, Turnbull BW. eds. Group sequential tests with application to clinical trials. Boca Raton: Chapman and Hall/CRC, 2000.
- Proschan MA, Hunsberger SA. Designed extension of studies based on conditional power. Biometrics 1995;51:1315-24. [PubMed]
- Shen Y, Fisher L. Statistical inference for self-designing clinical trials with a one-sided hypothesis. Biometrics 1999;55:190-7. [PubMed]
- Tsiatis AA, Mehta C. On the inefficiency of the adaptive design for monitoring clinical trials. Biometrika 2003;90:367-78.
- Thall PF, Simon R. Practical Bayesian guidelines for phase IIB clinical trials. Biometrics 1994;50:337-49. [PubMed]
- Thall PF, Simon R, Estey EH. Bayesian sequential monitoring designs for single-arm clinical trials with multiple outcomes. Stat Med 1995;14:357-79. [PubMed]
- Thall PF, Wooten L, Tannir N. Monitoring event times in early phase clinical trials: some practical issues. Clin Trials 2005;2:467-78. [PubMed]
- Lee JJ, Liu DD. A predictive probability design for phase II cancer clinical trials. Clin Trials 2008;5:93-106. [PubMed]
- Pocock SJ, Simon R. Sequential treatment assignment with balancing for prognostic factors in the controlled clinical trials. Biometrics 1975;31:103-15. [PubMed]
- Efron B. International Symposium on Hodgkin's Disease. Session 6. Survival data and prognosis. Invited discussion: Forcing a sequential experiment to be balanced. Natl Cancer Inst Monogr 1973;36:571-2. [PubMed]
- Zelen M. Play the winner rule and the controlled clinical trial. J Am Stat Assoc 1969;64:131-46.
- Wei LJ, Durham S. The randomized play-the-winner rule in medical trials. J Am Stat Assoc 1978;73:840-3.
- Rosenberger WF, Stallard N, Ivanova A, et al. Optimal adaptive designs for binary response trials. Biometrics 2001;57:909-13. [PubMed]
- Eisele JR. The doubly adaptive biased coin design for sequential clinical trials. Journal of Statistical Planning and Inference 1994;38:249-61.
- Hf F, Zhang LX. Asymptotic properties of doubly adaptive biased coin designs for multitreatment clinical trials. Ann Statist 2004;32:268-301.
- Thall PF, Wathen KJ. Practical Bayesian adaptive randomisation in clinical trials. Eur J Cancer 2007;43:859-66. [PubMed]
- Lee JJ, Gu XM, Liu SY. Bayesian adaptive randomization designs for targeted agent development. Clin Trials 2010;7:584-96. [PubMed]
- Yin G, Chen N, Lee JJ. Phase II trial design with Bayesian adaptive randomization and predictive probability. J R Stat Soc Ser C Appl Stat 2012;61: [PubMed]
- Korn EL, Freidlin B. Outcome--adaptive randomization: is it useful? J Clin Oncol 2011;29:771-6. [PubMed]
- Lee JJ, Chen N, Yin G. Worth adapting? Revisiting the usefulness of outcome-adaptive randomization. Clin Cancer Res 2012;18:4498-507. [PubMed]
- Berry DA, Muller P, Grieve AP, et al. Adaptive Bayesian designs for dose-ranging drug trials, In: Gatsonis C, Kass RE, Carlin B, et al. eds. Case Studies in Bayesian Statistics, Volume V. New York: Springer-Verlag, 2001.
- Wason JM, Trippa L. A comparison of Bayesian adaptive randomization and multi-stage designs for multi-arm clinical trials. Statistics in Medicine 2014;33:2206-21. [PubMed]
- Gooley TA, Martin PJ, Fisher LD, et al. Simulation as a design tool for phase I/II clinical trials: an example from bone marrow transplantation. Control Clin Trials 1994;15:450-62. [PubMed]
- Thall PF, Russell KE. A strategy for dose-finding and safety monitoring based on efficacy and adverse outcomes in phase I/II clinical trials. Biometrics 1998;54:251-64. [PubMed]
- O'Quigley J, Hughes MD, Fenton T. Dose-finding designs for HIV studies. Biometrics 2001;57:1018-29. [PubMed]
- Yin G, Li Y, Ji Y. Bayesian dose-finding in phase I/II trials using toxicity and efficacy odds ratio. Biometrics 2006;62:777-84. [PubMed]
- Huang X, Biswas S, Oki Y, et al. A parallel phase I/II clinical trial design for combination therapies. Biometrics 2007;63:429-36. [PubMed]
- Yuan Y, Yin G. Bayesian phase I/II drug-combination trial design in oncology. Ann Appl Stat 2011;5:924-42. [PubMed]
- Hoering A, LeBlanc M, Crowley J. Seamless phase I-II trial design for assessing toxicity and efficacy for targeted agents. Clin Cancer Res 2011;17:640-6. [PubMed]
- Inoue LYT, Thall P, Berry DA. Seamlessly expanding a randomized phase II trial to phase III. Biometrics 2002;58:823-31. [PubMed]
- Huang X, Ning J, Li Y, et al. Using short-term response information to facilitate adaptive randomization for survival clinical trials. Stat Med 2009;28:1680-9. [PubMed]
- Stallard N. A confirmatory seamless phase II/III clinical trial design incorporating short-term endpoint information. Stat Med 2010;29:959-71. [PubMed]
- Kimani PK, Stallard N, Hutton JL. Dose selection in seamless phase II/III clinical trials based on efficacy and safety. Stat Med 2009;28:917-36. [PubMed]
- Bischoff W, Miller F. A seamless phase II/III design with sample-size reestimation. J Biopharm Stat 2009;19:595-609. [PubMed]
- Wason J, Magirr D, Law M, et al. Some recommendations for multi-arm multi-stage trials. Stat Methods Med Res 2013. [Epub ahead of print]. [PubMed]
- Sydes MR, Parmar MK, James ND, et al. Issues in applying multi-arm multi-stage methodology to a clinical trial in prostate cancer: the MRC STAMPEDE trial. Trials 2009;10:39. [PubMed]
- Sawyers C. Targeted cancer therapy. Nature 2004;432:294-7. [PubMed]
- Sledge GW. What is targeted therapy? J Clin Oncol 2005;23:1614-15. [PubMed]
- Mandrekar SJ, Sargent DJ. Clinical trial designs for predictive biomarker validation: theoretical considerations and practical challenges. J Clin Oncol 2009;27:4027-34. [PubMed]
- Freidlin B, McShane LM, Korn EL. Randomized clinical trials with biomarkers: design issues. J Natl Cancer Inst 2010;102:152-60. [PubMed]
- Sargent DJ, Mandrekar SJ. Statistical issues in the validation of prognostic, predictive, and surrogate biomarkers. Clin Trials 2013;10:647-52. [PubMed]
- Mandrekar SJ, Sargent DJ. A review of phase II trial designs for initial marker validation. Contemp Clin Trials 2013;36:597-604. [PubMed]
- Sargent D, Allegra C. Issues in clinical trial design for tumor marker studies. Semin Oncol 2002;29:222-30. [PubMed]
- Sargent DJ, Conley BA, Allegra C, et al. Clinical trial designs for predictive marker validation in cancer treatment trials. J Clin Oncol 2005;23:2020-27. [PubMed]
- Sinicrope FA, Sargent DJ. Molecular pathways: microsatellite instability in colorectal cancer: prognostic, predictive, and therapeutic implications. Clin Cancer Res 2012;18:1506-12. [PubMed]
- Simon R, Maitournam A. Perspective evaluating the efficiency of targeted designs for randomized clinical trials. Clin Cancer Res 2004;10:6759-63. [PubMed]
- Maitournam A, Simon R. On the efficiency of targeted clinical trials. Stat Med 2005;24:329-39. [PubMed]
- Freidlin B, Simon R. Evaluation of randomized discontinuation design. J Clin Oncol 2005;23:5094-98. [PubMed]
- Simon R. The use of genomics in clinical trial design. Clin Cancer Res 2008;14:5984-93. [PubMed]
- Willyard C. “Basket studies” will hold intricate data for cancer drug approvals. Nat Med 2013;19:655. [PubMed]
- Lillie EO, Patay B, Diamant J, et al. The n-of-1 clinical trial: the ultimate strategy for individualizing medicine? Per Med 2011;8:161-73. [PubMed]
- Friends of Cancer Research (2013) Design of a lung cancer master protocol. Available online: http://www.focr.org/events/design-lung-cancer-master-protocol
- Simon R. Biomarker based clinical trial design. Chin Clin Oncol 2014;3:39.
- Zhou X, Liu S, Kim ES, et al. Bayesian adaptive design for targeted therapy development in lung cancer-a step toward personalized medicine. Clin Trials 2008;5:181-93. [PubMed]
- Kim ES, Herbst RS, Wistuba II, et al. The BATTLE Trial: Personalizing therapy for lung cancer. Cancer Discov 2011;1:44-53. [PubMed]
- Berry DA, Herbst RS, Rubin EH. Reports from the 2010 Clinical and Translational Cancer Research Think Tank meeting: design strategies for personalized therapy trials. Clin Cancer Res 2012;18:638-44. [PubMed]
- Barker AD, Sigman CC, Kelloff GJ, et al. I-SPY 2: An adaptive breast cancer trial design in the setting of neoadjuvant chemotherapy. Clin Pharmacol Ther 2009;86:97-100. [PubMed]
- Carrie P. I-SPY 2 breast cancer clinical trial launches nationwide. Cancer 2010;116:3308.
- Quantum Leap (2013) I-SPY 2 Trial graduates 2 new drugs. Available online: http://www.quantumleaphealth.org/spy-2-trial-graduates-2-new-drugs-press-release/
- Lee JJ, Chen N. Software for design of clinical trials. In: Crowley J, Hoering A. eds. Handbook of Statistics in Clinical Oncology, 3rd ed. Boca Raton, FL: Chapman and Hall/CRC Press, 2011.
- Chow SC, Chang M. Adaptive design methods in clinical trials -- a review. Orphanet J Rare Dis 2008;3:11. [PubMed]
- Gaydos B, Anderson KM, Berry D, et al. Good practices for adaptive clinical trials in pharmaceutical product development. Drug Inf J 2009;43:539-56.


