The current design of oncology phase I clinical trials: progressing from algorithms to statistical models
Editor’s note:
The special column “Statistics in Oncology Clinical Trials” is dedicated to providing state-of-the-art review or perspectives of statistical issues in oncology clinical trials. Our Chairs for the column are Dr. Daniel Sargent and Dr. Qian Shi, Division of Biomedical Statistics and Informatics, Mayo Clinic, Rochester, MN, USA. The column is expected to convey statistical knowledge which is essential to trial design, conduct, and monitoring for a wide range of researchers in the oncology area. Through illustrations of the basic concepts, discussions of current debates and concerns in the literature, and highlights of evolutionary new developments, we are hoping to engage and strengthen the collaboration between statisticians and oncologists for conducting innovative clinical trials. Please follow the column and enjoy.
Introduction
Phase I trials are studies in humans to determine the highest dose possible of a cytotoxic or biologically targeted agent that can be administered to humans before an unacceptable rate of side effects occur. These side effects are known as dose-limiting toxicities (DLTs) and vary depending upon the type of cancer and the specific agent under study. These DLTs must be explicitly defined before the study begins and are often a subset of the Grade 3 and 4 toxicities outlined in the Common Terminology Criteria for Adverse Events (CTCAE) developed by the Cancer Therapy Evaluation Program (CTEP) of the National Cancer Institute (NCI). The current version of the CTCAE can be found at http://evs.nci.nih.gov/ftp1/CTCAE/About.html. Note that toxicities do not have to be life-threatening or irreversible to be considered DLTs; they simply have to be severe enough to cause termination of treatment with that dose of the agent. Another crucial aspect of defining DLTs is that, optimally, there is a specific way of identifying that the dose of the agent under study is a direct cause of the DLT. For example, thrombocytopenia is a possible side effect seen in patients receiving an allogeneic bone marrow transplant (BMT). As a result, defining Grade 4 thrombocytopenia as a DLT for a new agent under study in patients receiving an allogeneic BMT will be problematic if the actual source of the thrombocytopenia (BMT or agent) cannot be identified.
Once the DLTs have been clearly defined, investigators must determine the number of doses to study, as well as what those doses might be. Typically the lowest dose is a dose that is expected to have a very low probability, in the range of 5-10%, of causing DLTs in patients. Higher doses should have increasing expected rates of DLTs, with one of the doses having a DLT rate of π, a value between 0 and 1, which is the targeted rate of DLTs for the dose known as the maximum tolerated dose (MTD). The value of π is sometimes referred to as the targeted toxicity level (TTL). Of course, the actual DLT rates of the doses are unknown, and it is possible that there will be one or two doses that have DLT rates above the TTL. As a result, three doses is an absolute minimum number of doses to study in a phase I trial, with an upper bound on the number of doses dependent upon the number of patients that can be enrolled in the trial. Also note that the clinical values of the doses are not used directly in most Phase I trial designs, so that it is not necessarily important to have a wide range of dose values under study. What is more important is to have a range of doses whose DLT rates are expected to have a detectable amount of variation around the TTL. For example, if we have four doses of 50, 100, 200, and 500 mg/m2 and the TTL is π =0.30, identifying the MTD among those four doses will be very difficult if their true DLT rates are 0.25, 0.27, 0.30, and 0.35, and much easier if their true DLT rates are 0.08, 0.20, 0.30, and 0.45, due to the larger variation in the latter set of DLT rates.
When designing a phase I trial, it must be kept in mind that there are two, likely conflicting, goals for the study: (I) the global goal of correctly identifying the MTD at the end of the study and improving treatment of future patients; and (II) the local goal of treating as many patients as possible in the current trial at the MTD. Thus, phase I trial designs are comprised of two distinct parts: (I) a set of decision rules for determining the dose assignment of each patient during the study; and (II) a method to estimate the MTD at the end of the trial using the data collected during the trial. The ideal trial would be one that assigns every patient to the same dose and that dose is the MTD. However, assigning every patient to the same dose would supply no information about the other doses if the dose administered was not the MTD. Thus, we need to vary the dose assignments among patients in order to gain information about where the MTD may actually lie among the doses. However, by doing so, we naturally cannot assign every patient to the dose we currently believe is the MTD and we sacrifice the benefit of individual patients for the sake of the success of the entire trial. We now discuss three classes of traditional phase I trial designs, a summary of which can be found in Table 1.
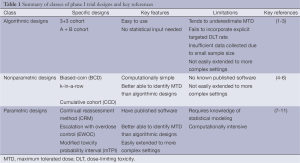
Full table
First steps: algorithmic designs
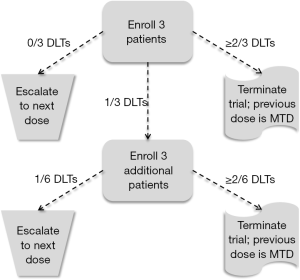
Because phase I trials occur at the earliest stage of developing new cytotoxic agents, the number of patients enrolled in a phase I trial is traditionally quite low and is driven more by the amount of resources, such as time, money, and availability of patients, than a statistical goal, such as power or confidence interval width. As a result, although an estimate of the MTD is determined at the end of the trial, the variability of this estimate is relatively large. The 3+3 cohort method (1) is the most common design used in phase I trials, and is a member of a more general set of designs known as A + B cohort designs, whose statistical properties have been examined in detail (2). In the 3+3 algorithm, patients are enrolled in cohorts of three patients, with each patient in the cohort receiving the same dose. Patients of the first cohort are assigned to a dose (Dose 1, i.e., the lowest dose) and followed for pre-defined period of time (e.g., first cycle of the treatment) for the occurrence of a DLT. If no patients experience DLTs, a new cohort of three patients is enrolled and assigned to Dose 2. If one patient experiences a DLT, a new cohort of three patients is enrolled and assigned to Dose 1. If one or more additional patients experience DLTs (two or more among all six patients receiving Dose 1), accrual is terminated. And if two or more patients in the first cohort of three patients experience DLT, accrual is also terminated. The MTD is then defined as one dose lower than the dose last assigned in the study when accrual was terminated. Figure 1 contains a diagram of the 3+3 algorithm.
Although the simplicity of the 3+3 algorithm continues to motivate its use in contemporary phase I trials, there are several failings of the 3+3 cohort method that give powerful evidence against its use in practice (3). First, the 3+3 cohort method has no explicit objective in mind, other than to find a dose that gives an observed DLT rate of no more than 33%. At its conclusion, the 3+3 cohort method produces data that give no confidence in what the actual DLT rate of any of the dose levels might be, and thus little confidence in the selected MTD. For example, the first three columns of Table 2 contain information on the number of patients and the number of DLTs observed in a hypothetical trial of three doses. Given these results, Dose 2 would be selected as the MTD. However, the final column contains the exact 95% confidence intervals for the true DLT rates of the three doses. These confidence intervals demonstrate several facts. First, the DLT rate of Dose 3 could be as low as 0.09, which would be seen as an acceptable DLT rate in most clinical settings. Second the DLT rate of Dose 2 (the MTD) could be as high as 0.64, which is a DLT rate that would be seen as unacceptable in most clinical settings. Third, there is a vast amount of overlap among all three confidence intervals, suggesting there is no evidence that any difference exists among the DLT rates of the three doses. In other words, strong conclusions are made during the trial using very weak evidence. Finally, it is mistakenly believed that the 3+3 algorithm is associated with a TTL of 0.33. However, the DLT rate targeted is actually closer to 0.22 (12). Thus, not only is the 3+3 algorithm inflexible, it can only be used for one specific TTL, and that TTL is rather conservative for most cytotoxic agents. Since it is commonly accepted that lower toxicity also indicates lower efficacy, the 3+3 algorithm will often produce an MTD that will fail to demonstrate suitable efficacy when studied in phase II trials.

Full table
Second steps: statistically-based improvements
Nonparametric designs
The 3+3 algorithm is a distant relative of up-and-down designs (13-15). By the name of the designs, the dose assigned to a future cohort of patients can go up or down from the dose assigned to the current cohort of patients, based upon the observed DLT rate in the current cohort. This property also demonstrates a major flaw of the 3+3 algorithm: it never allows for a new cohort of patients to be assigned to a lower dose once excessive DLTs are observed in the current cohort. Instead, the trial is stopped altogether. Although de-escalation could be implemented in the 3+3 algorithm, such a feature is rarely, if ever, used in practice.
One example of a feasible up-and-down design for oncology phase I trials is the biased- coin design (BCD) (16). This design enrolls patients individually (in cohorts of size one). If the current patient is assigned to a dose and experiences a DLT, the next patient is assigned to the next lowest dose. If instead the current patient does not experience a DLT, the next patient can be assigned to either (I) the current dose or (II) the next highest dose. This decision is decided by the flip of a biased coin, which is a coin with probability ph of heads and (1-ph) of tails. If the coin comes up heads, the next patient is assigned to the next highest dose, and if the coin comes up tails, the next patient is assigned to the current dose. This process is continued until a pre-determined number of patients have been enrolled. Figure 2 contains a diagram of the BCD. Another competing design is the k-in-a-row design (4), in which the design does not allow for dose escalation until k consecutive patients, all of whom are assigned to the same dose, do not experience DLT. The abilities of the BCD and the k-in-a-row designs to identify the MTD have been formally examined and compared via simulation (5,17).

Since all up-and-down designs produce what is known statistically as a Markov Chain, statistical theory demonstrates that there is a limiting distribution to the dose assignments of the BCD, i.e., if we know the true DLT rates of the doses and the TTL, we can compute the percentage of patients that will be assigned on average to each dose. More importantly, it can be shown that using the BCD leads to the largest percentages of patients assigned to doses with DLT rates close to the value ph/(1+ph). In other words, given a TTL of π, the BCD should use a biased coin with probability of heads ph = π/(1 − π), for π ≤0.5. For example, if the TTL is 0.30, then ph =3/7≈0.43. In general, as the TTL gets closer to zero, the value of ph also gets closer to zero in order to limit escalation and assignment of overly toxic doses. One specific form of the BCD was suggested by Dixon and Mood over sixty years ago (18) in which the biased coin has probability ph =1, i.e., two consecutive patients will never be assigned to the same dose since escalation must occur in the absence of a DLT.
If investigators wish to enroll patients in cohorts rather than individually, then the exact decision rules for up-and-down designs become less obvious. For example, one might consider enrolling three patients to a dose with the following decisions for the next cohort: (I) if two or three DLTs, assign to next lowest dose; (II) if zero or one DLT, flip a biased coin and assign to next highest dose if heads or current dose if tails. However, this decision rule is not unique and others are possible. To help provide a more systematic set of decision rules with up-and-down designs with any size cohorts, Ivanova, Flournoy, and Chung proposed the cumulative cohort design (6), which essentially removes the use of a biased coin and creates decision rules for dose assignments (escalate, remain, or deescalate) based upon the accumulated proportion of DLTs observed among all enrolled patients, rather than only the current cohort.
Parametric designs
In contrast to the nonparametric approach of up-and-down designs, the continual reassessment method (CRM) was the first parametric, model-based approach proposed specifically for use in oncology phase I trials (7), and was later given practical improvements that have been adopted in practice (19,20). In the CRM, the probabilities of DLT for each of the doses are assumed to be fully explained by a one-parameter model that is a function of the value of each dose. If there are J doses in the study and we let dj denote the value of dose j= 1, 2, …, J, then two of the most commonly-used functions in the CRM are: (I) the logistic model f(dj;β) = exp[3 + exp(β)dj]/[1 + exp(3 + exp(β)dj)] and; (II) the so-called “power” model f(dj;β) = exp(β)dj, which β is the unknown parameter. As intimated earlier, the actual values given to each dose are not their actual clinical values, but are values chosen for computational convenience.
To operationalize, the CRM requires a prior guess as to what one might think the DLT rate is for each dose, which we denote as pj. The vector (p1, p2, …, pJ) of prior guesses is known more commonly as the “skeleton,” and the skeleton is used to determine the value to use for each dose: the dose values are dj = log(pj) − log(1 − pj) − 3 for the logistic model and dj = pj with the empiric model. For example, if we are studying four doses and we believe the DLT rates might be 0.05, 0.10, 0.20, and 0.40, respectively, then the dose values would be –5.9 –5.2 –4.4, and –3.4, respectively, for the logistic model, and 0.05, 0.10, 0.20, and 0.40, respectively, for the empiric model.
The underlying principle of the CRM is that the dose assignment for each patient (or cohort of patients) should be determined from the model by using the data collected during the trial to sequentially estimate the model parameter, β, the value of which then produces estimates of the DLT rates for each of the doses. The dose whose DLT rate is currently closest to the TTL is then selected as the dose assigned to future patients until more data is collected and an updated estimate of β is determined. As the trial proceeds, the dose assignments begin to approach a neighborhood of the MTD so that patients near the end of the trial are likely to be assigned to a dose that is the MTD, or at least close to the MTD. And once the trial ends, β is estimated using all the data from the trial and the model is used to determine the dose with DLT rate closest to the TTL; this dose is the MTD. Although the CRM was initially proposed using Bayesian methods to estimate β, a maximum-likelihood approach was later published (21). An excellent tutorial on the CRM was published (8); a schematic representation of the CRM from (22) is shown in Figure 3.
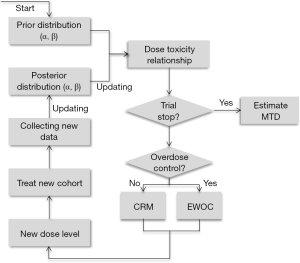
In the Bayesian formulation of the CRM, there are two components needed to estimate β: (I) the data, specifically the dose assignment and indicator of DLT or no DLT for each patient; and (II) the prior distribution for β, which gives a range of plausible values for β, and is usually a normal distribution centered around zero with variance σ2. The utility of Bayesian methods is that early in the trial, when little data exists, the prior plays a much greater role in estimation of β than the data, while later in the trial, sufficient data has been collected so that estimation of β is based primarily on the data and very little weight is given to the prior. The relative weights given to the data and the prior are largely determined by the value of σ2; too large a value for σ2 will lead to instability of the CRM early in the trial, while too small a value for σ2 will lead to the data playing in insufficient role for estimation of β later in the trial. Due to a historical lack of systematic methods to determine a value σ2, the only real option is to simulate data under a variety of settings and a variety of values for σ2 until one value of σ2 appears to lead to suitable ability of identifying the MTD across all settings. However, recent work has been done to provide a more systematic approach to calibrate σ2 at the beginning of the trial (23), as well as adaptively adjusting the value of σ2 during the study (24).
An approach similar to the CRM is known as Escalation With Overdose Control (EWOC) (9). Like the CRM, EWOC adopts a parametric model for the relationship of dose and probability of DLT and a prior distribution is placed on the parameter to facilitate estimation. However, instead of assigning each patient to the dose whose DLT rate is currently estimated to be closest to the TTL, EWOC instead examines the cumulative probability that the DLT rate of each dose is above the TTL and assigns a dose whose probability of overdosing remains below a specified threshold. Thus, the goal of EWOC is to identify the MTD at the end of the study while formally limiting the number of patients exposed to toxic doses during the study. However, the CRM and EWOC have identical statistical frameworks, and a unified CRM-EWOC design also exists (25).
Even with the multitude of published research demonstrating the superiority of the CRM over the 3+3 algorithm [see (26) for a recent example], the CRM continues to have limited use in actual clinical trials due to the perceived statistical and computational complexity of these methods, leading many to view the dose assignment decisions of the CRM as coming from a ‘black box’. As an attempt to connect the simplicity of an algorithmic approach with the statistical foundation of parametric methods, Ji et al. developed a design called the modified toxicity probability interval method (mTPI) (10). Like an algorithm, the dose assignment decision rules for a trial using the mTPI can be outlined in a spreadsheet at the beginning of the study, unlike the CRM, in which dose assignments are contingent upon the actual outcomes that occur during the trial. However, like the CRM, the decision rules in the mTPI design are founded in Bayesian statistical theory by assuming each DLT rate has a Beta distribution. A simulation-based comparison of the mTPI with the 3+3 algorithm was recently published and demonstrates the superiority of the mTPI design to the 3+3 algorithm (11).
Future steps: moving beyond simple dose-finding
Time-to-event and ordinal outcomes
One limitation of the designs described thus far is that each enrolled patient must be completely followed for DLT before a dose assignment decision can be made for future patients. In reality, a new patient may become eligible for enrollment before all enrolled subjects have completed their follow-up. Although some solutions to this issue were suggested for the CRM (7), the time-to-event CRM (TITE-CRM) (27) was the first formal attempt to incorporate the time-to-event nature of DLTs into the model used by the CRM. The TITE-CRM essentially includes the follow-up of patients still under observation for DLT as a weight whose value is the completed amount of follow-up relative to their planned amount of follow-up. For example, in a trial in which patients are planned to be followed for eight weeks, a patient who has completed four weeks of follow-up without DLT would contribute half as much data as a patient who completed all eight weeks of follow-up without DLT. Although many incorrectly view these weights as ad-hoc, they are actually based upon the assumption that DLTs occur uniformly during the follow-up period and are generated from what is known statistically as a cure model (28). Since these weights can lead to over-escalation when DLTs are not uniform and instead occur rather late in the follow-up period, a generalization to the TITE-CRM exists in which the weights are adaptive and change depending upon when DLTs are actually occurring in the trial (28).
An alternative generalization to the TITE-CRM is to compute the predictive probability that future patients will be exposed to doses that are later determined to be overly toxic (29). If this probability is too large, accrual to the trial is suspended until more follow-up is obtained on enrolled subjects and the risk of assignment of future patients to toxic doses is lowered. Although such an approach will reduce the observed rate of DLTs in the presence of late-onset DLTs with the TITE-CRM, it also will prolong the length of the trial depending upon the frequency and duration of accrual suspensions. Recently another approach has been suggested for addressing incomplete follow-up, known as the EM-CRM (30). This design views partially-followed patients as having missing data (their DLT outcome is unknown) and uses the expectation-maximization (EM) algorithm to estimate the model parameter β. It is likely that both the TITE-CRM and EM-CRM have similar large-sample properties, i.e., as more and more patients are enrolled, both methods lead to similar estimates of the MTD, but a head-to-head comparison of the two approaches via simulations using realistic sample sizes has yet to be done.
Since DLTs are binary realizations of what was originally a graded ordinal variable, it might seem that there is a loss of information when using a binary outcome rather than an ordinal one. If a dose was associated with a measurable amount of Grade 1 and 2 toxicities, which would have been coded as no DLT in the original CRM, this information might be useful in determining the probability of Grade 3 and 4 toxicities with that same dose. Therefore, ordinal regression models have been suggested as a way of generalizing the CRM to handle more than two categories of toxicity (31,32); a similar approach for EWOC has also been proposed (33). However, existing work seems to suggest that identification of the MTD using ordinal outcomes offers little improvement over the traditional approach with binary outcomes (34).
Multiple outcomes
If the circumstances of a trial allow a determination of treatment efficacy within the same time frame required to assess toxicity, it seems sensible that toxicity and efficacy should both be considered when selecting a dose for further study. Such considerations are also important when the relationship between dose and toxicity and/or efficacy is not monotonic. A number of authors have proposed designs in which both outcomes (toxicity and efficacy) are modeled as a function of dose. Both models are then used to determine dose assignments by estimating the DLT and efficacy rates of each dose and selection of the dose whose rates are closest to the TTL and the targeted efficacy level (TEL), respectively. However, often one dose may be preferred in terms of toxicity, while another may be preferred in terms of efficacy. Thus, investigators must determine the relative importance of the outcomes to each other when deciding the dose assignment for each patient. Specifically, if a dose has a DLT rate that is above the TTL but its efficacy rate is also above the TEL, should this dose be assigned to patients? Conversely, if a dose has a DLT rate below the TTL but also has an efficacy rate below the TEL, should this dose be assigned to patients? Furthermore, there will be doses in which one outcome has a rate below its corresponding target and one above its corresponding target, further complicating the decision of assigning those doses.
Mathematically, one approach is to compute for each dose the distance of the rates of DLT and efficacy from their corresponding targets and compute a weighted average of those two distances and select the dose that has the smallest average (35). A weighted-outcome approach also was used in a recent trivariate CRM design in which the third outcome is a surrogate for efficacy when follow-up for efficacy may be quite long and a surrogate marker could be measured earlier (36). Both of these approaches require input from investigators as to what the appropriate weights each outcome should receive. Equal weights should be used when there are ambivalent opinions as to the relative importance each outcome and several weights have been proposed (35,36).
An alternate approach is to place a utility, which is a score from 0 to 100, on each of the four possible combinations of toxicity (yes/no) and efficacy (yes/no), with higher utility indicating a more desirable pair of outcomes (37). Based upon the data collected in the trial, Bayesian methods are used to determine which dose has the largest expected utility and that dose is assigned to the next patient. As with the weighted distance approach described previously, this method also requires input from investigators to determine what utility value should be assigned to each pair of outcomes. Specifically, although efficacy with no DLT would be the most desirable pair of outcomes and the one with greatest utility and no efficacy with DLT would be the least desirable pair of outcomes and the one with least utility, it is not clear (I) how to order the other two pairs of outcomes; and (II) how much variability the four utility values should have among each other. A related approach that uses odds ratios rather than utilities to order the four pairs of outcomes has been proposed (38).
Two-agent combinations and multiple administrations
Another recent extension of the CRM is to generalize the model using a single parameter to quantify the effects of a single agent on the probability of DLT to a model that includes additional parameters to quantify the effects of (I) another agent; or (II) additional administrations of the same agent. One can view a two-agent study as a search over a grid, in which each row corresponds to each dose of one agent and each column corresponds to the dose of the other agent. Each square of the grid is a combination whose DLT rate is unknown and the goal is to extend the modeling framework of the CRM and apply it to the DLT rates of the combinations in the grid. Unfortunately, the addition of another agent greatly increases the mathematical complexity of the models that have been proposed.
Early approaches attempted to extend the one-parameter model of the CRM to a multi-parameter model that includes, at a minimum, one parameter each for the doses of the two agents (39-41). Additional parameters can also be incorporated to increase flexibility of the model and account for any possible synergistic or antagonistic effects the two agents may have with regard to DLT. However, it has been suggested that these additional interaction parameters do not appear to be necessary, mostly due to the small amount of data collected during a Phase I trial relative to the number of model parameters that need to be estimated (40,41).
Alternative models have been proposed that have a foundation in copulas (42,43), which are statistical models for the joint probability of DLT of both agents that is a function of the individual (marginal) probabilities of DLT for each agent when given alone, as well as a correlation parameter that expresses the synergistic or antagonistic relationship of the agents. Regardless of the model used, all the cited methods mimic the CRM in that dose assignments are adaptively determined from the data by updating estimates of the model parameters and the probabilities of DLT for every dose of one of the agents in combination with every dose of the other agent, with each enrolled patient receiving the current estimate of the maximum tolerated combination (MTC), the combination whose estimated DLT probability is closest to the TTL.
Given that the mathematical complexity of existing two-agent designs may limit their use in application, two methods have been recently published that attempt to directly use the CRM framework as a way to assess the toxicity profile of two agents. One approach is the generalized CRM (gCRM) (44), in which all doses of one agent, referred to as Agent A, are studied in combination with one of the doses of the other agent (Agent B). Essentially, the CRM is used to examine the doses of Agent A, with a separate CRM for the combination of Agent A with each dose of Agent B. These separate CRM models all have the same parameter (i.e., slope) quantifying how the different doses of Agent A relate to the probability of DLT. However, all the models contain an extra parameter (i.e., intercept) that are allowed to differ among the models to incorporate the differential effects of the doses of Agent B on the probability of DLT. Bayesian methods are used to “connect” all the intercepts to each other in order to use all the data collected in the study to estimate the intercepts and determine the MTC.
The other approach is the partial order CRM (POCRM) (45,46), in which a combination of two doses is viewed as single dose whose probability of DLT is modeled directly in the CRM. However, by doing so, the CRM must be constrained to reflect the natural ordering of the DLT rates of the combinations during the estimation of parameters and determination of the combination to assign to each patient. For example, suppose we have two doses of Agent A (A1 and A2) and two doses of Agent B (B1 and B2), with 1 denoting a lower dose than 2. Although one can envision that the combination of A1 and B1 will have the lowest DLT rate, and the combination of A2 and B2 will have the highest DLT rate among all four combinations, it is less obvious how to rank the DLT rates of the combinations of A1 with B2 and A2 with B1. The POCRM proposes methods to incorporate this so-called “partial” order into the CRM algorithm.
The CRM in its original form was designed to address the probability of DLT for a single administration and was insufficient for assessing the cumulative effects of an agent on the probability of DLT. To that end, an extension was proposed in which DLT is viewed as a time-to-event outcome and the hazard of each administration is modeled as a parametric function of dose (47-49). The joint hazard for multiple administrations is assumed to be the sum of the hazards of each of the individual administrations and this sum quantifies the cumulative effect of multiple administrations, as well as their timing, i.e., weekly, bi-weekly, monthly, etc. Like the TITE-CRM, these approaches incorporate the time to DLT (rather than a binary indicator of DLT) and thus allow for new patients to be enrolled once they are eligible, regardless of the amount of follow-up collected on previously enrolled patients.
However, the methods just cited assume that the dose and number of administrations assigned to patients cannot change once they were enrolled in the study. Such an assumption conflicts with actual practice, whereby within-patient changes to dose and/or number of administrations may be warranted. For example, suppose a patient has completed half of their assigned administrations when the data from other patients are analyzed and indicate that this patient’s number of administrations at the same dose is now believed to be overly toxic. Investigators may wish to terminate further administrations for this patient or continue with the planned administrations, but with a lower dose. These additional decision rules, if formally implemented into the design and dose-assignment algorithm, would complicate the actual use of dose and schedule finding designs in practice, although a formal design that incorporates within-patient dose and/or schedule changes has been recently created (50). In addition, an extended design that incorporates both efficacy and toxicity for dose and schedule finding has been proposed recently (51).
Discussion
Since the inception of the CRM, the variety of possible designs for Phase I studies has grown quickly and investigators now have at their disposal excellent statistically-framed designs for a variety of early-phase clinical trials. However, algorithmic designs like the 3+3 cohort method and other ad-hoc approaches continue to be the designs of choice in current published Phase I trials. The disappointedly low use of up-and-down and model-based designs in actual trials has been discussed in recent systematic reviews (52,53), although there are a handful of trials that are exceptions to this trend (54,55). It is believed that the statistical complexity, and relative dearth of user-friendly software, for statistically sophisticated designs is the major reason that they are not used more routinely. However, a number of textbooks covering phase I trial designs have been published in the past few years (56-59), and it is hoped that with a greater readership and increased promotion of statistical packages for the model-based designs will increase their use and place the 3+3 method in a position of disfavor.
One unresolved issue for model-based designs remains how to determine the sample size necessary for a Phase I trial. Although by design the 3+3 cohort method has a maximum sample size equal to six patients/dose, none of the up-and-down nor model-based designs have had formal methods developed for sample size calculation except to use simulations. The one exception lies with the CRM, for which an approach for computing suitable sample sizes has been proposed (60), although the core of the computations still requires simulations.
A current debate in phase I trial design is whether or not assigning each patient to the current estimate of the MTD is the best approach to use. There have been suggestions that asymptotically, i.e., in very large sample sizes, assigning each patient to the current estimate of the MTD, known as “greedy” or “myopic” dose assignments, does not provide 100% certainly that the study will correctly identify the MTD at the end of the study (61,62). Although it is unclear how this result relates to actual phase I trials, which enroll a relatively small number of patients, some have begun to propose that each patient not be assigned the current estimate of the MTD, but should instead be randomized to receive either the current estimate of the MTD or doses in a neighborhood of the estimated MTD. Such a concept may prove to be beneficial to the end result of the trial, namely improving identification of the MTD, but certainly comes with a cost, since each patient is now given the chance to receive a dose that is sub-optimal, at least based upon the data from the trial at that point. No clear consensus yet exists on whether or not randomization within Phase I trials should be a standard part of the design.
The most recent application of existing phase I trial designs is with biologic and molecularly targeted agents (MTAs). Unlike anti-cancer agents, whose toxicity is assumed to increase with dose, biologic agents and MTAs tend to have a low probability of DLT among all doses and the probability of DLT does not necessarily increase with dose and may actually plateau after a certain dose. Thus, one is not interested in the maximum dose whose DLT rate is close to the TTL, but the lowest dose among those with DLT rates close to the TTL, the so-called minimum effective dose (MED) or biologically optimal dose (BOD). Existing methodology for dose-finding of biologic agents and MTAs is quite limited, but novel work is slowly being developed and it is expected that numerous designs will be published in the coming years.
Acknowledgements
Disclosure: The author declares no conflict of interest.
References
- Storer BE. Design and analysis of phase I clinical trials. Biometrics 1989;45:925-37. [PubMed]
- Lin Y, Shih WJ. Statistical properties of the traditional algorithm-based designs for phase I cancer clinical trials. Biostatistics 2001;2:203-15. [PubMed]
- Ahn C. An evaluation of phase I cancer clinical trial designs. Stat Med 1998;17:1537-49. [PubMed]
- Oron AP, Hoff PD. The k-in-a-row up-and-down design, revisited. Stat Med 2009;28:1805-20. [PubMed]
- Ivanova A, Montazer-Haghighi A, Mohanty SG, et al. Improved up-and-down designs for phase I trials. Stat Med 2003;22:69-82. [PubMed]
- Ivanova A, Flournoy N, Chung Y. Cumulative cohort design for dose-finding. J Stat Plan Inference 2007;137:2316-27.
- O’Quigley J, Pepe M, Fisher L. Continual reassessment method: a practical design for phase 1 clinical trials in cancer. Biometrics 1990;46:33-48. [PubMed]
- Garrett-Mayer E. The continual reassessment method for dose-finding studies: a tutorial. Clin Trials 2006;3:57-71. [PubMed]
- Babb J, Rogatko A, Zacks S. Cancer phase I clinical trials: efficient dose escalation with overdose control. Stat Med 1998;17:1103-20. [PubMed]
- Ji Y, Liu P, Li Y, Bekele BN. A modified toxicity probability interval method for dose-finding trials. Clin Trials 2010;7:653-63. [PubMed]
- Ji Y, Wang SJ. Modified toxicity probability interval design: a safer and more reliable method than the 3 + 3 design for practical phase I trials. J Clin Oncol 2013;31:1785-91. [PubMed]
- Ivanova A. Escalation, group and A + B designs for dose-finding trials. Stat Med 2006;25:3668-78. [PubMed]
- Durham SD, Flournoy N. Up-and-down designs. I. Stationary treatment distributions. Lect Notes Monogr Ser 1995;25:139-57.
- Durham S, Flournoy N. Up-and-down designs. II. Exact treatment moments. Lect Notes Monogr Ser 1995;25:158-78.
- Giovagnoli A, Pintacuda N. Properties of frequency distributions induced by general ‘up-and-down’ methods for estimating quantiles. J Stat Plan Inference 1998;74:51-63.
- Stylianou M, Flournoy N. Dose finding using the biased coin up-and-down design and isotonic regression. Biometrics 2002;58:171-7. [PubMed]
- Liu S, Cai C, Ning J. Up-and-down designs for phase I clinical trials. Contemp Clin Trials 2013;36:218-27. [PubMed]
- Dixon WJ, Mood AM. A method for obtaining and analyzing sensitivity data. J Am Stat Assoc 1948;43:109-26.
- Faries D. Practical modifications of the continual reassessment method for phase I cancer clinical trials. J Biopharm Stat 1994;4:147-64. [PubMed]
- Goodman SN, Zahurak ML, Piantadosi S. Some practical improvements in the continual reassessment method for phase I studies. Stat Med 1995;14:1149-61. [PubMed]
- O’Quigley J, Shen LZ. Continual reassessment method: a likelihood approach. Biometrics 1996;52:673-84. [PubMed]
- Chen Z, Zhao Y, Cui Y, et al. Kowalski. Methodology and application of adaptive and sequential approaches in contemporary clinical trials. J Probab Stat 2012;2012:1-20.
- Lee SM, Cheung YK. Calibration of prior variance in the Bayesian continual reassessment method. Stat Med 2011;30:2081-9. [PubMed]
- Zhang J, Braun TM, Taylor JM. Adaptive prior variance calibration in the Bayesian continual reassessment method. Stat Med 2013;32:2221-34. [PubMed]
- Chu PL, Lin Y, Shih WJ. Unifying CRM and EWOC designs for phase I cancer clinical trials. J Stat Plan Inference 2009;139:1146-63.
- Iasonos A, Wilton AS, Riedel ER, et al. A comprehensive comparison of the continual reassessment method to the standard 3 + 3 dose escalation scheme in Phase I dose-finding studies. Clin Trials 2008;5:465-77. [PubMed]
- Cheung YK, Chappell R. Sequential designs for phase I clinical trials with late-onset toxicities. Biometrics 2000;56:1177-82. [PubMed]
- Braun TM. Generalizing the TITE-CRM to adapt for early- and late-onset toxicities. Stat Med 2006;25:2071-83. [PubMed]
- Bekele BN, Ji Y, Shen Y, et al. Monitoring late-onset toxicities in phase I trials using predicted risks. Biostatistics 2008;9:442-57. [PubMed]
- Yuan Y, Yin G. Robust EM continual reassessment method in oncology dose finding. J Am Stat Assoc 2011;106:818-31. [PubMed]
- Van Meter EM, Garrett-Mayer E, Bandyopadhyay D. Proportional odds model for dose-finding clinical trial designs with ordinal toxicity grading. Stat Med 2011;30:2070-80. [PubMed]
- Van Meter EM, Garrett-Mayer E, Bandyopadhyay D. Dose-finding clinical trial design for ordinal toxicity grades using the continuation ratio model: an extension of the continual reassessment method. Clin Trials 2012;9:303-13. [PubMed]
- Tighiouart M, Cook-Wiens G, Rogatko A. Escalation with overdose control using ordinal toxicity grades for cancer phase I clinical trials. J Probab Stat 2012;2012:1-18.
- Iasonos A, Zohar S, O’Quigley J. Incorporating lower grade toxicity information into dose finding designs. Clin Trials 2011;8:370-9. [PubMed]
- Braun TM. The bivariate continual reassessment method. extending the CRM to phase I trials of two competing outcomes. Control Clin Trials 2002;23:240-56. [PubMed]
- Zhong W, Koopmeiners JS, Carlin BP. A trivariate continual reassessment method for phase I/II trials of toxicity, efficacy, and surrogate efficacy. Stat Med 2012;31:3885-95. [PubMed]
- Thall PF, Cook JD. Dose-finding based on efficacy-toxicity trade-offs. Biometrics 2004;60:684-93. [PubMed]
- Yin G, Li Y, Ji Y. Bayesian dose-finding in phase I/II clinical trials using toxicity and efficacy odds ratios. Biometrics 2006;62:777-84. [PubMed]
- Thall PF, Millikan RE, Mueller P, et al. Dose-finding with two agents in Phase I oncology trials. Biometrics 2003;59:487-96. [PubMed]
- Wang K, Ivanova A. Two-dimensional dose finding in discrete dose space. Biometrics 2005;61:217-22. [PubMed]
- Braun TM, Wang S. A hierarchical Bayesian design for phase I trials of novel combinations of cancer therapeutic agents. Biometrics 2010;66:805-12. [PubMed]
- Yin G, Yuan Y. Bayesian dose finding in oncology for drug combinations by copula regression. J R Stat Soc Ser C Appl Stat 2009;58:211-24.
- Yin G, Yuan Y. A latent contingency table approach to dose finding for combinations of two agents. Biometrics 2009;65:866-75. [PubMed]
- Braun TM, Jia N. A generalized continual reassessment method for two-agent Phase I trials. Stat Biopharm Res 2013;5:105-15. [PubMed]
- Wages NA, Conaway MR, O’Quigley J. Continual reassessment method for partial ordering. Biometrics 2011;67:1555-63. [PubMed]
- Wages NA, Conaway MR, O’Quigley J. Dose-finding design for multi-drug combinations. Clin Trials 2011;8:380-9. [PubMed]
- Braun TM, Yuan Z, Thall PF. Determining a maximum-tolerated schedule of a cytotoxic agent. Biometrics 2005;61:335-43. [PubMed]
- Braun TM, Thall PF, Nguyen H, et al. Simultaneously optimizing dose and schedule of a new cytotoxic agent. Clin Trials 2007;4:113-24. [PubMed]
- Liu CA, Braun TM. Parametric non-mixture cure models for schedule finding of therapeutic agents. J R Stat Soc Ser C Appl Stat 2009;58:225-36. [PubMed]
- Zhang J, Braun TM. A Phase I Bayesian adaptive design to simultaneously optimize dose and schedule assignments both between and within patients. J Am Stat Assoc 2013;108: [PubMed]
- Thall PF, Nguyen HQ, Braun TM, et al. Using joint utilities of the times to response and toxicity to adaptively optimize schedule-dose regimes. Biometrics 2013;69:673-82. [PubMed]
- Rogatko A, Schoeneck D, Jonas W, et al. Translation of innovative designs into phase I trials. J Clin Oncol 2007;25:4982-6. [PubMed]
- Le Tourneau C, Lee JJ, Siu LL. Dose escalation methods in phase I cancer clinical trials. J Natl Cancer Inst 2009;101:708-20. [PubMed]
- Muler JH, McGinn CJ, Normolle D, et al. Phase I trial using a time-to-event continual reassessment strategy for dose escalation of cisplatin combined with gemcitabine and radiation therapy in pancreatic cancer. J Clin Oncol 2004;22:238-43. [PubMed]
- de Lima M, Giralt S, Thall PF, et al. Maintenance therapy with low-dose azacitidine after allogeneic hematopoietic stem cell transplantation for recurrent acute myelogenous leukemia or myelodysplastic syndrome: a dose and schedule finding study. Cancer 2010;116:5420-31. [PubMed]
- Chevret S. eds. Statistical Methods for Dose-Finding Experiments. Wiley and Sons, 2006.
- Cheung YK. eds. Dose Finding by the Continual Reassessment Method. New York: Chapman. & Hall/CRC Press, 2011.
- Berry SM, Carlin BP, Lee JJ, et al. eds. Muller. Bayesian Adaptive Methods for Clinical Trials. Chapman and Hall/CRC, 2011.
- Yin G. eds. Clinical Trial Design: Bayesian and Frequentist Adaptive Methods. Wiley and Sons, 2012.
- Kuen Cheung Y. Sample size formulae for the Bayesian continual reassessment method. Clin Trials 2013;10:852-61. [PubMed]
- Azriel D, Mandel M, Rinott Y. The treatment versus experimentation dilemma in dose finding studies. J Stat Plan Inference 2011;141:2759-68.
- Oron AP, Azriel D, Hoff PD. Dose-finding designs: the role of convergence properties. Int J Biostat 2011;7:39. [PubMed]


